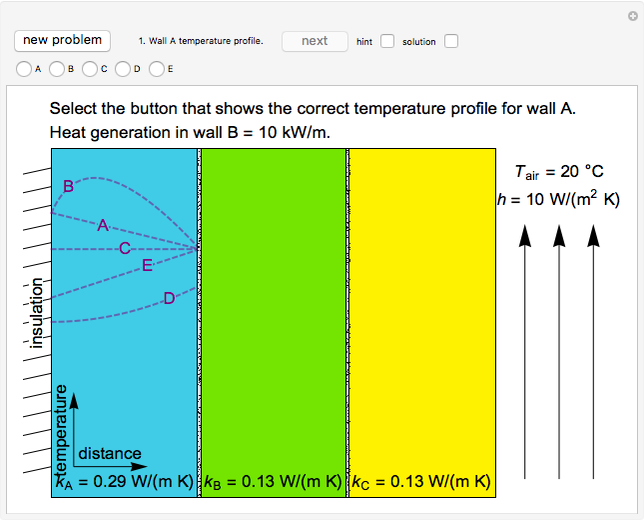
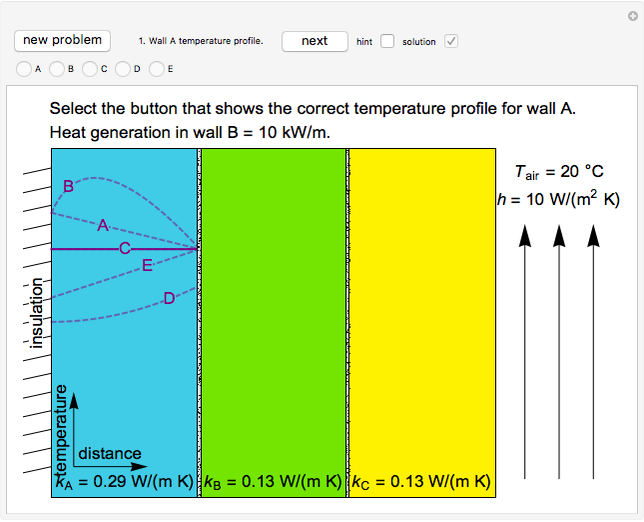
Identify Temperature Profiles for Heat Generation or Conduction through Composite Walls

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
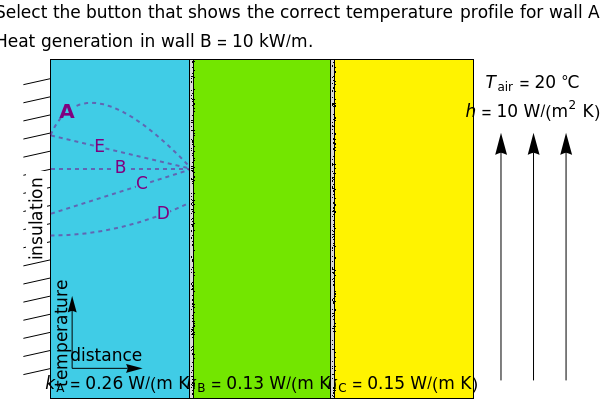
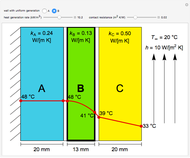
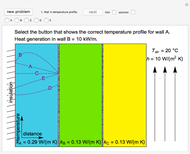
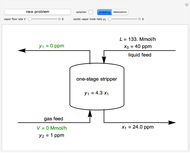
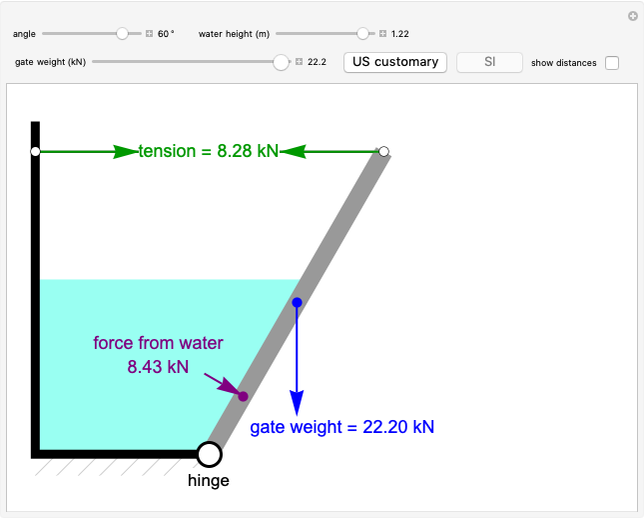
Heat is generated at a constant rate in either wall 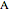 or
or 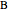 (whichever wall is slowly changing color intensity). The object of this Demonstration is to identify the correct steady-state temperature profile in each wall. The thermal conductivity for each wall is indicated on the figure, and the contact resistance between the walls is given. The left side of wall
(whichever wall is slowly changing color intensity). The object of this Demonstration is to identify the correct steady-state temperature profile in each wall. The thermal conductivity for each wall is indicated on the figure, and the contact resistance between the walls is given. The left side of wall 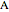 is insulated and heat is transferred from the right side of wall
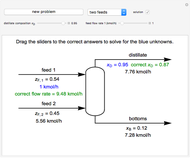
is insulated and heat is transferred from the right side of wall  to flowing air at 20 °C. Use buttons to select the correct temperature profile for each wall in sequence; check the "hint" box for help. Once you select a temperature profile for a wall, you must check "solution" before clicking the "next" button; you cannot move backward. Click the "new problem" button to start over with a new set of conditions.
to flowing air at 20 °C. Use buttons to select the correct temperature profile for each wall in sequence; check the "hint" box for help. Once you select a temperature profile for a wall, you must check "solution" before clicking the "next" button; you cannot move backward. Click the "new problem" button to start over with a new set of conditions.
Contributed by: Rachael L. Baumann and Neil Hendren (November 2018)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Details
$FailedSnapshots
Permanent Citation