Conduction through a Composite Wall

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
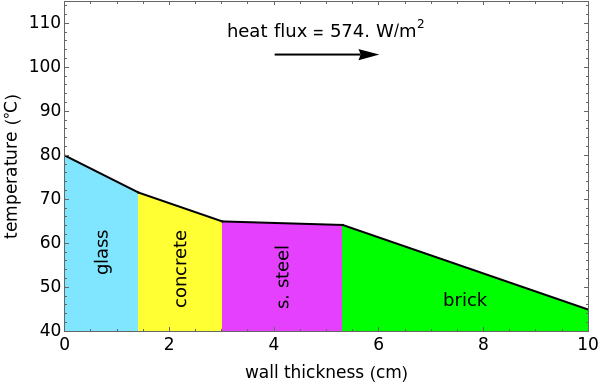
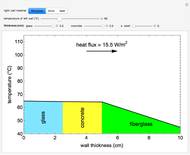
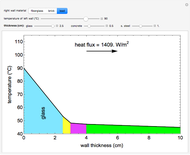
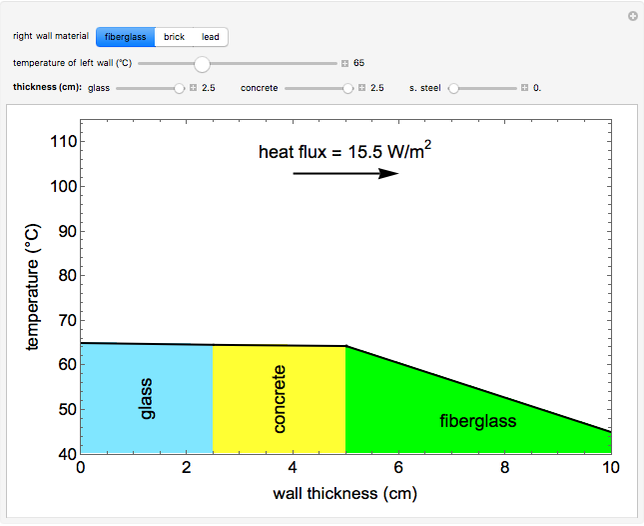
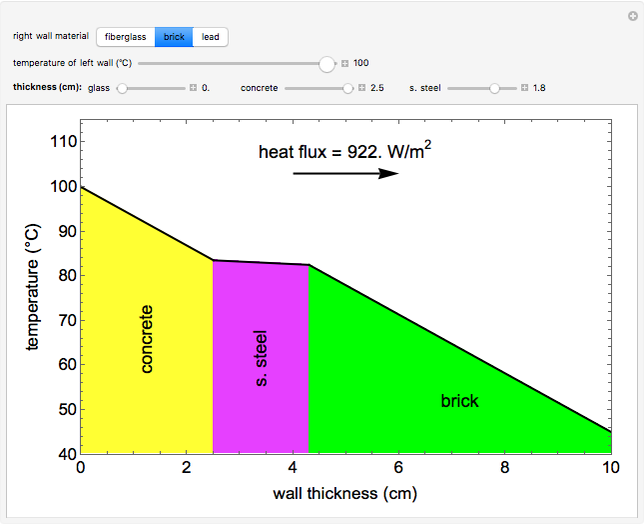
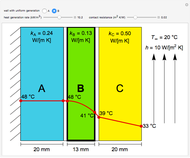
This Demonstration calculates temperature profiles and the heat flux for steady-state conduction through four walls in series; the total wall thickness is 10 cm. Change the temperature of the left wall with a slider; the temperature of the right wall is fixed at 45°C. Change the thicknesses of the first three walls with sliders. Use buttons to select the composition of the end wall (fiberglass, brick, or lead). The heat flux is the same through each wall.
Contributed by: Mathew L. Williams and Rachael L. Baumann (March 2014)
Additional contributions by: John L. Falconer and Nick Bongiardina
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
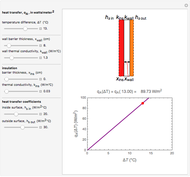
The steady-state heat flux for four walls in series was calculated from the total heat-transfer resistance. The flux is the same for each wall (since there is no heat generation), and thus the flux equation can be applied to each wall. The heat flux, conductivities, wall thicknesses, and the wall temperatures were used to determine the temperatures at the interfaces between walls.
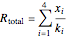 ,
,
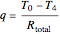 ,
,
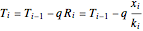 ,
,
where 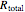 is the total thermal resistance (
is the total thermal resistance (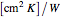 ),
), 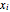 is the wall thickness (cm),
is the wall thickness (cm), 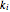 is thermal conductivity (W/[cm K]),
is thermal conductivity (W/[cm K]),  is heat flux (
is heat flux ( ),
),  is temperature (°C), and
is temperature (°C), and 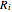 is the thermal resistance for conduction (
is the thermal resistance for conduction (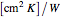 ).
).
The screencast video at [1] works through a problem to calculate temperatures in a composite wall.
Reference
[1] Thermal Circuits: Temperatures in a Composite Wall [Video]. (Jan 6, 2012) www.youtube.com/watch?v=HZI65RuGa4M.
Permanent Citation