The Perturbed Rat

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
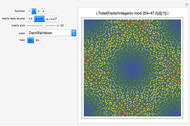
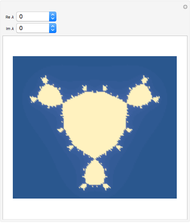
Recently, Blanchard, Devaney, Garijo, and Russell have studied rational maps of the form  , where
, where  and
and  are complex-valued parameters. This Demonstration considers the special case when
are complex-valued parameters. This Demonstration considers the special case when  and
and  . When both the real and imaginary parts of
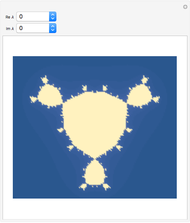
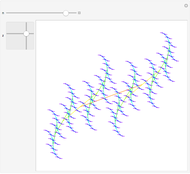
. When both the real and imaginary parts of  are equal to zero, we obtain a Julia set called "the rat". When
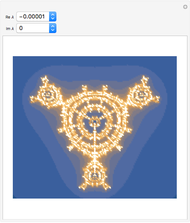
are equal to zero, we obtain a Julia set called "the rat". When  is nonzero, there is a pole of order three at the origin that changes the structure of the Julia set and perturbs the rat.
is nonzero, there is a pole of order three at the origin that changes the structure of the Julia set and perturbs the rat.
Contributed by: Elizabeth Russell, Sebastian Marotta, and Jeff Hamrick (March 2011)
Based on work by: Paul Blanchard, Bob Devaney, Antonio Garijo, and Elizabeth Russell
Open content licensed under CC BY-NC-SA
Snapshots
Details
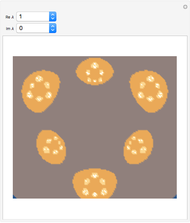
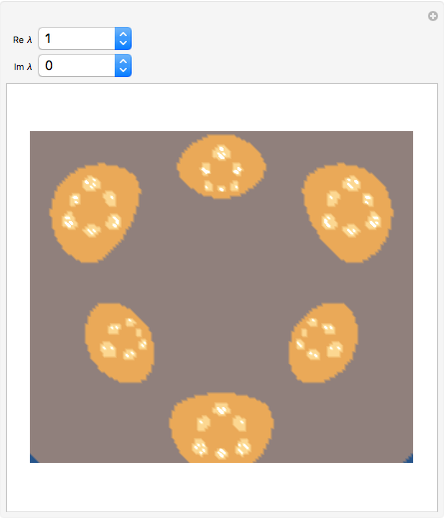
When  is sufficiently small, the Julia set has a structure analogous to a Cantor set of simple, closed curves for the map
is sufficiently small, the Julia set has a structure analogous to a Cantor set of simple, closed curves for the map  , for
, for  . This family of maps ("the rat maps") generalizes a result of Kurt McMullen.
. This family of maps ("the rat maps") generalizes a result of Kurt McMullen.
To make higher-quality pictures, download the source notebook, increase the number of iterates, and decrease the step size used to create the mesh of points in the complex plane.
P. Blanchard, R. L. Devaney, A. Garijo, and E. Russell, "A Generalized Version of the McMullen Domain," International Journal of Bifurcation and Chaos, 18(8), 2008 pp. 2309–2318.
Permanent Citation