Acceptance/Rejection Sampling

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
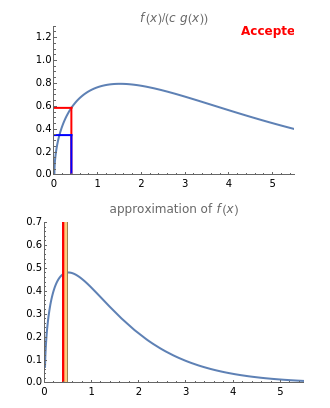
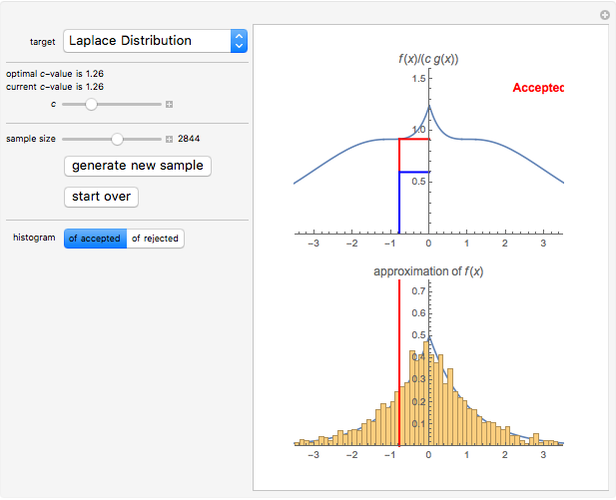
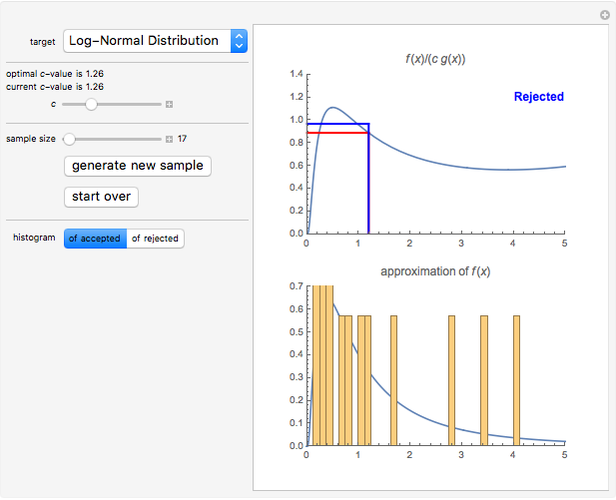
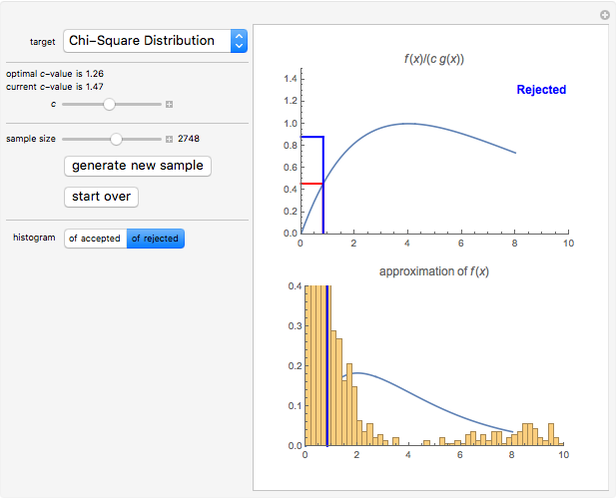
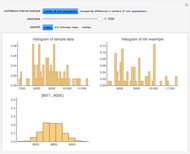
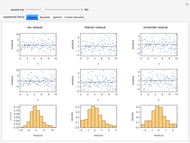
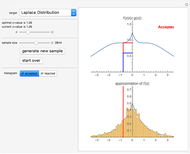
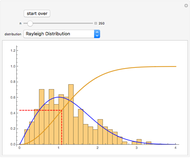
With this Demonstration, you can visualize the rejection sampling technique, which is also known as the acceptance-rejection algorithm. Select a target distribution (the distribution from which you would like to generate random samples) and then choose a "threshold value"  that influences the likelihood that a candidate sample from a nontarget distribution will be "accepted" as if it were, in fact, from the target distribution. You can change the number of random variates generated and view histograms of both the accepted and the rejected samples.
that influences the likelihood that a candidate sample from a nontarget distribution will be "accepted" as if it were, in fact, from the target distribution. You can change the number of random variates generated and view histograms of both the accepted and the rejected samples.
Contributed by: Ryan Carroll and Jeff Hamrick (September 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Suppose that you want to generate pseudorandom numbers from a random variable 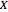 with probability distribution
with probability distribution 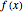 , but that other methods (like the method of inverse transforms) do not work well (perhaps because the cumulative distribution function associated with
, but that other methods (like the method of inverse transforms) do not work well (perhaps because the cumulative distribution function associated with 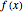 does not have an explicit inverse). Instead, choose a companion random variable
does not have an explicit inverse). Instead, choose a companion random variable 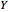 with probability density function
with probability density function 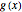 , making sure that
, making sure that 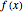 and
and 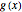 have the same support (i.e. both vanish and fail to vanish over the same sets of real numbers).
have the same support (i.e. both vanish and fail to vanish over the same sets of real numbers).
Ideally, the random variable 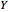 has been chosen in such a way that the cumulative distribution function associated with
has been chosen in such a way that the cumulative distribution function associated with 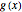 has an explicit inverse and is easy to simulate using a technique like the method of inverse transforms.
has an explicit inverse and is easy to simulate using a technique like the method of inverse transforms.
The acceptance-rejection algorithm is then as follows: (1) independently simulate a random number  with a uniform distribution over the unit interval and a realization
with a uniform distribution over the unit interval and a realization 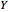 * of the random variable
* of the random variable 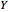 ; and then (2) using a fixed, strictly positive number
; and then (2) using a fixed, strictly positive number  , accept
, accept 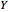 * as a realization of
* as a realization of 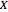 if
if 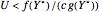 , where
, where 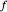 and
and  are the probability densities of the random variables
are the probability densities of the random variables 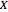 and
and 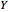 , respectively. If
, respectively. If 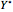 is not accepted, it is rejected. This process is continued repeatedly until a target number of realizations of
is not accepted, it is rejected. This process is continued repeatedly until a target number of realizations of 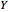 is generated.
is generated.
Heuristically, the acceptance-rejection method works particularly efficiently when certain conditions are satisfied. First, the target random variable 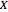 and the companion random variable
and the companion random variable 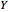 should have density functions that "look" as similar as possible. In this Demonstration, we use the exponential random variable as a companion random variable for the probability distributions with support on the positive part of the real line (the gamma distribution, chi-square distribution, half-normal distribution, and log-normal distribution). We use the Cauchy distribution as the companion distribution for the probability distributions with support over the whole real line (the normal distribution, the Student t distribution, the Gumbel distribution, and the Laplace distribution).
should have density functions that "look" as similar as possible. In this Demonstration, we use the exponential random variable as a companion random variable for the probability distributions with support on the positive part of the real line (the gamma distribution, chi-square distribution, half-normal distribution, and log-normal distribution). We use the Cauchy distribution as the companion distribution for the probability distributions with support over the whole real line (the normal distribution, the Student t distribution, the Gumbel distribution, and the Laplace distribution).
Second, the strictly positive constant  influences the tendency of the algorithm to "accept" instead of "reject". If
influences the tendency of the algorithm to "accept" instead of "reject". If  is particularly large,
is particularly large,  will be less than
will be less than  with small probability, and the algorithm will throw away many fine proxies for
with small probability, and the algorithm will throw away many fine proxies for 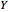 . On the other hand, if
. On the other hand, if  is particularly close to zero and
is particularly close to zero and 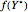 is not substantially smaller than
is not substantially smaller than 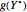 , then
, then 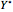 will probably be accepted. It can be shown that the acceptance-rejection algorithm produces an empirical distribution of pseudorandom numbers that converges the most rapidly to the target distribution if
will probably be accepted. It can be shown that the acceptance-rejection algorithm produces an empirical distribution of pseudorandom numbers that converges the most rapidly to the target distribution if  is chosen to be the maximum possible value of
is chosen to be the maximum possible value of 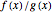 over the (common) support of
over the (common) support of 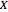 and
and 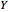 .
.
The acceptance-rejection method can be generalized to the Metropolis–Hastings algorithm and is a type of Markov chain Monte Carlo simulation. For further information about the acceptance-rejection algorithm, see [1] or [2].
References
[1] S. M. Ross, Simulation, 4th ed., Boston: Elsevier, 2006.
[2] S. Ghahramani, Fundamentals of Probability, with Stochastic Processes, 3rd ed., New York: Prentice Hall, 2004.
Permanent Citation