Missing Voters

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Suppose that on a proposed bill there are  voters, of whom
voters, of whom 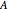 are against the bill. Suppose also that
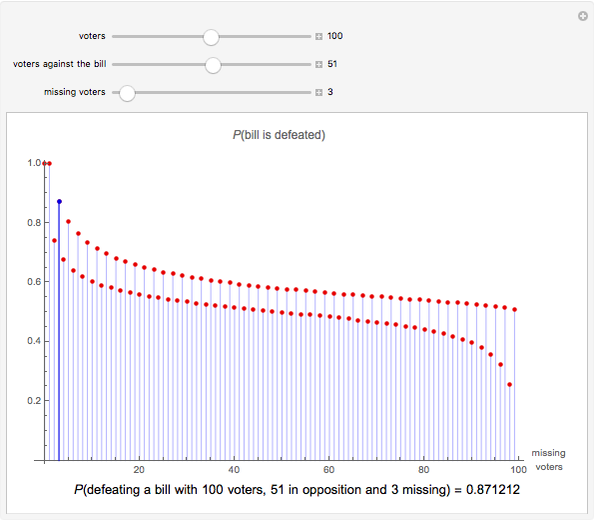
are against the bill. Suppose also that 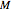 voters will miss the vote. Assume that the missing voters are absent for purely random reasons (traffic delays, illness, forgetfulness, etc.) that have nothing to do with whether they are for or against the bill. What is the probability that the bill will be defeated? This Demonstration shows these probabilities. We assume that, in the case of a tie, the bill passes.
voters will miss the vote. Assume that the missing voters are absent for purely random reasons (traffic delays, illness, forgetfulness, etc.) that have nothing to do with whether they are for or against the bill. What is the probability that the bill will be defeated? This Demonstration shows these probabilities. We assume that, in the case of a tie, the bill passes.
Contributed by: Heikki Ruskeepää (February 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
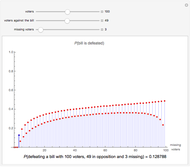
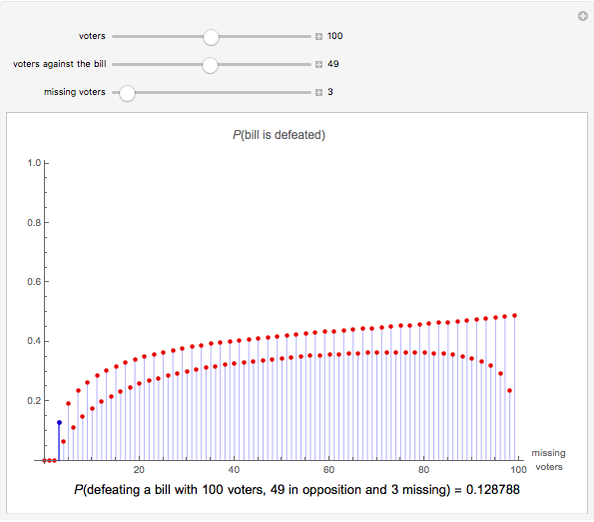
Snapshot 1: The figure shows the probabilities that the bill is defeated with 100 voters, of whom 49 are against the bill, 51 are for the bill, and 0, 1, 2, …, 100 voters are missing. For example, if 3 voters are missing, the probability is 0.128788; if 4 voters are missing, the probability is 0.0637301; and if 5 voters are missing, the probability is 0.193846. If 0, 1, or 2 voters are missing, the bill will never be defeated. For example, if 1 voter is missing, that voter is, in the worst case, for the bill, so that we have 49 against and 50 for the bill. If 2 voters are missing, they are, in the worst case, both for the bill, so that we have 49 against and 49 for; in this case the bill is accepted.
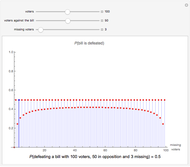
Snapshot 2: Now we have 50 voters against the bill and 50 for it. If an odd number of voters is missing, the probability that the bill is defeated is 0.5. For example, if 1 voter is missing, that voter is equally likely to be for as against the bill.
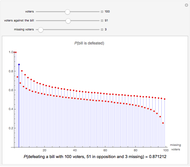
Snapshot 3: We have 51 against and 49 for the bill. The probability that the bill is defeated is 1 if 0 or 1 voter is missing.
Recall that we have a total of 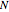 voters, of whom
voters, of whom 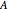 voters are against the bill and
voters are against the bill and  voters are for the bill. Also,
voters are for the bill. Also, 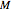 voters are missing. Let
voters are missing. Let 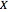 be the random variable that is the number of voters missing the vote who, if present, would have voted for the bill. Then we have
be the random variable that is the number of voters missing the vote who, if present, would have voted for the bill. Then we have 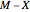 voters missing the vote who would have voted against the bill. Therefore, we have
voters missing the vote who would have voted against the bill. Therefore, we have  voters for the bill and
voters for the bill and 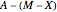 against the bill. The bill will be defeated if
against the bill. The bill will be defeated if 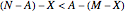 or
or 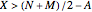 . This condition can also be written as
. This condition can also be written as 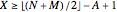 , where
, where 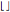 is used for the floor function (the greatest integer less than or equal to the argument).
is used for the floor function (the greatest integer less than or equal to the argument).
The random variable 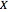 has the hypergeometric distribution. In Mathematica, this distribution has three parameters
has the hypergeometric distribution. In Mathematica, this distribution has three parameters  ,
, 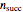 , and
, and 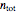 . The hypergeometric distribution gives the distribution of the number of successes in
. The hypergeometric distribution gives the distribution of the number of successes in  draws from a population of size
draws from a population of size 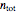 containing
containing 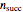 successes. Now we have
successes. Now we have 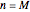 ,
, 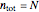 , and
, and 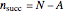 . Thus,
. Thus,
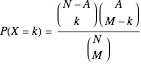 .
.
The probability that the bill is defeated is then
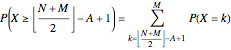 .
.
The bill is accepted if there are as many votes for the bill as there are against it.
The Demonstration is based on problem 11 in [1].
Reference
[1] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton: Princeton University Press, 2008.
Permanent Citation