Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Caged Anharmonic Oscillator in the Causal Interpretation of Quantum Mechanics

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

This Demonstration studies the caged anharmonic oscillator—fundamental for quantum field theory as well as many-body theory—in the causal interpretation of quantum mechanics developed by David Bohm. Among the large number of possible potentials for the Schrödinger equation, only a very few are analytically solvable. The potential is that of the harmonic oscillator 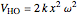with rational frequency ratio, but additionally with a barrier term from inclusion of a repulsive force [1].

[more]

The analytic solutions of the wavefunction are polynomials in the spatial variable of rational or irrational order, depending on the parameter . In the causal interpretation, every particle has a definite position and momentum at all times, but the trajectories are not measurable directly. The particles are guided by a quantum potential, which follows from the amplitude of the wavefunction. As an example, only a superposition of two eigenstates with their corresponding eigenenergies is chosen. In the graphic on the left, you can see the position of the particles, the squared wavefunction (blue), the potential (orange), the quantum potential (red), and the velocity (green). On the right, the graphic shows the squared wavefunction plus trajectories. The velocity, the quantum potential, and the classical potential are scaled to fit.

[less]

Contributed by: Klaus von Bloh (July 2012)
Open content licensed under CC BY-NC-SA

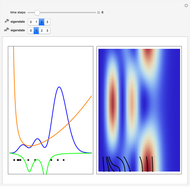
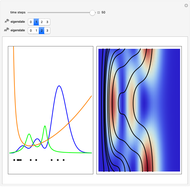
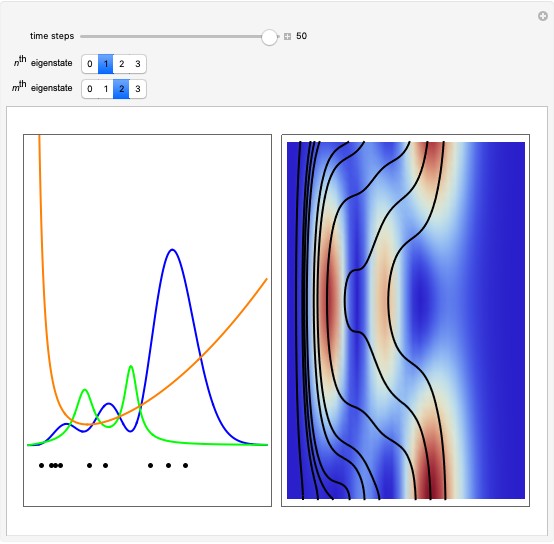
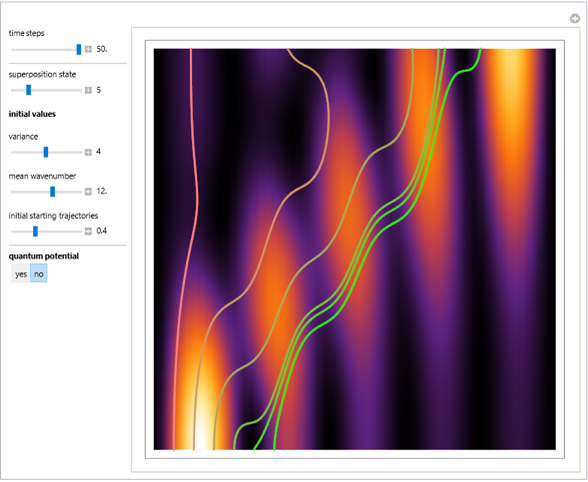
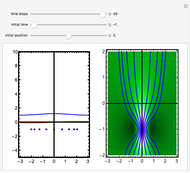
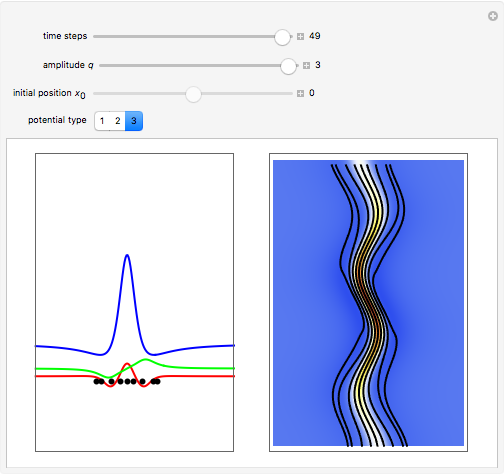
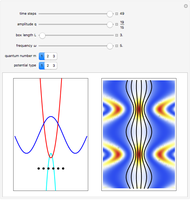
Snapshots

Details

The simplified Schrödinger equation is:

, with , and so on, where is a complex-valued function and are real-valued constants. Here the common standard notation is used, where is the time and is the spatial coordinate. The time-dependent unnormalized solution gives the wavefunction:

,

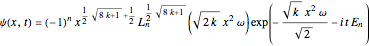where are the associated Laguerre polynomials and the quantized energy is given by 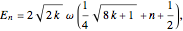where is an integer. For simplicity, the parameters and are set equal to 1 in the quantum potential. If 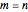, then the wave density is time independent and the particles are at rest. The guiding equation for the particle velocity is , which is calculated from the gradient of the phase from the total wavefunction in the eikonal form 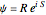. The quantum potential 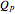is given by 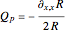. Due to limitations of CPU power, AccuracyGoal, PrecisionGoal, and MaxSteps are decreased. The starting positions of the particles are linearly distributed around the peaks of the wave density at

Reference

[1] N. W. Evans and P. E. Verrier, "Superintegrability of the Caged Anisotropic Oscillator," Journal of Mathematical Physics, 49(9), 2008 pp. 092902–092902-10. dx.doi.org/10.1063/1.2988133 or arxiv.org/abs/0808.2146.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send