Pressure of a Rotating Fluid

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
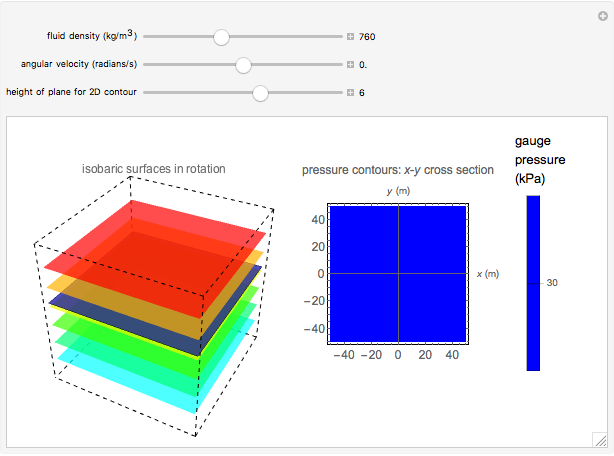
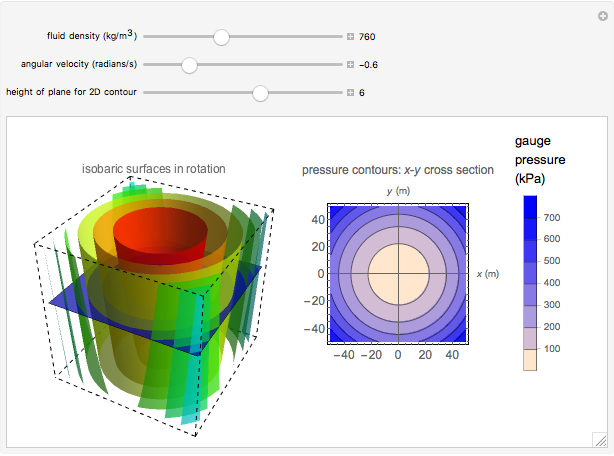
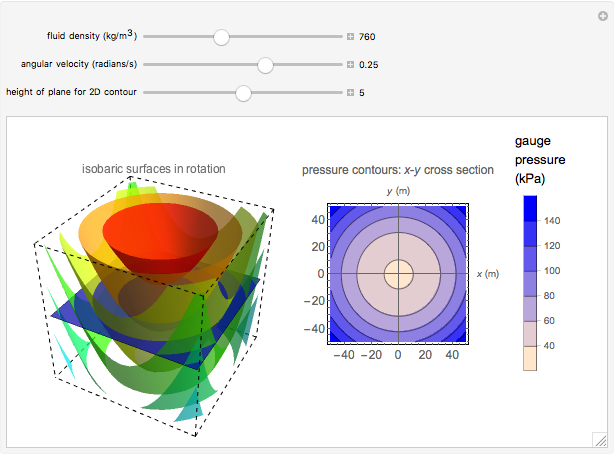
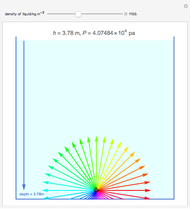
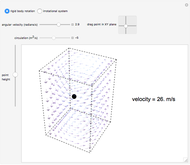
This Demonstration shows how the pressure in a fluid is affected by rotation at constant angular velocity. Use sliders to vary the fluid density and angular velocity. The 3D graph on the left shows the isobaric surfaces (surfaces of constant pressure) that result from the rotation. The graph on the right shows pressure contours taken from a cross section in the 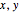 plane; a darker color indicates higher hydrostatic pressure. The cross section is represented by a blue plane on the 3D graph; select the height of the cross section with a slider. The pressure profile does not depend on the direction of the angular velocity. This physical situation is closely analogous to Newton's classic rotating-bucket experiment.
plane; a darker color indicates higher hydrostatic pressure. The cross section is represented by a blue plane on the 3D graph; select the height of the cross section with a slider. The pressure profile does not depend on the direction of the angular velocity. This physical situation is closely analogous to Newton's classic rotating-bucket experiment.
Contributed by: Megan Maguire and Rachael L. Baumann (January 2014)
Additional contributions by: Garret D. Nicodemus
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A fluid in a tank that rotates at a constant angular velocity about an axis (in this case about the  axis), rotates with the tank as a rigid body. The pressure gradient is written in cylindrical coordinates:
axis), rotates with the tank as a rigid body. The pressure gradient is written in cylindrical coordinates:
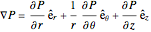 ,
,
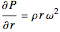 ,
,
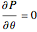 ,
,
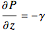 .
.
For this type of rigid body rotation, pressure is a function of  and
and  :
:
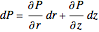 ,
,
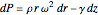 .
.
Integrating the last equation yields the pressure distribution:
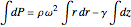 ,
,
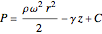 .
.
Along an isobaric surface (surface of constant pressure) 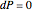 , so:
, so:
 ,
,
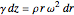 ,
,
integrating both sides yields the equation for surfaces at constant pressure:
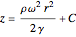 ,
,
since  , the equation is simplified to:
, the equation is simplified to:
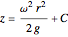 ,
,
where 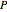 is the pressure in the fluid (Pa),
is the pressure in the fluid (Pa),  is the radial distance from the center (m),
is the radial distance from the center (m),  is distance from the tank bottom (m),
is distance from the tank bottom (m),  is fluid density (
is fluid density (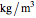 ),
),  is angular velocity (rad/s),
is angular velocity (rad/s),  is specific weight (
is specific weight (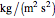 ),
),  is acceleration due to gravity,
is acceleration due to gravity, 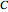 is a constant estimated as
is a constant estimated as 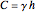 (
(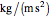 ), where
), where  is fluid height (m).
is fluid height (m).
Reference
[1] B. R. Munson, T. H. Okiishi, and W. W. Huebsch, Fundamentals of Fluid Mechanics, 6th ed., Hoboken, NJ: John Wiley & Sons, 2010.
Permanent Citation