Stable Marriages

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
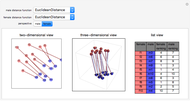
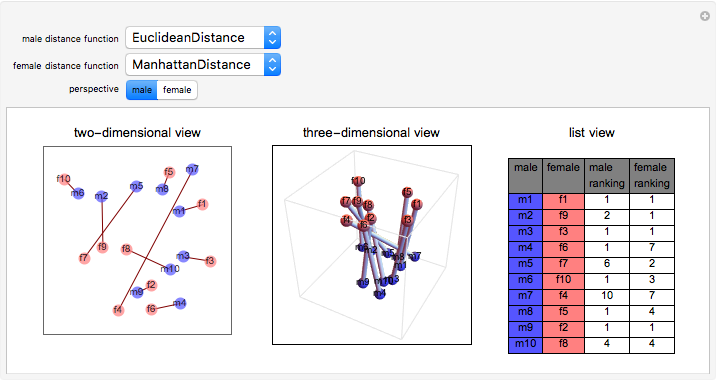
A set of marriages is unstable if a man and woman within the set could improve their happiness by marrying each other rather than staying with their current partners. This Demonstration shows the set of stable marriages that results from having the men rank females on the basis of a distance measure from themselves to each female. Reciprocally, the females rank the males on the basis of a distance measure from themselves to each male. As you move the males (blue) and the females (pink) around the leftmost graphic in the Demonstration, the moving person's rankings change and a potential exists for instability. The Demonstration shows the sets of stable marriages in three ways: (1) in the left graphic, the set of stable marriages is shown by lines between the spouses; (2) in the middle graphic, males in blue on the bottom are tied by a cylinder to their pink marital partner on the top; (3) the rightmost grid shows the sets of marriages and how each male ranks his female partner and how each female ranks her partner. You can change the distance function the males and females use for ranking and whether the male or female perspective on the matter will be taken.
Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
You can use this Demonstration in a recreational—and arguably villainous—fashion: take the part of a person who is currently matched with a spouse that the person ranked lowly. Figure out how the person could change his or her location or could move the location of romantic rivals so that a stable marriage would leave that person with a spouse more highly ranked.
For simplicity and in keeping with the historical formulation of this problem, this Demonstration excludes the interesting complication of homosexual romance.
A variant of the stable marriage algorithm is used to match applicants for medical residencies in the United States with hospitals using residents.
Permanent Citation
"Stable Marriages"
http://demonstrations.wolfram.com/StableMarriages/
Wolfram Demonstrations Project
Published: March 7 2011