Visualizing the Coarse Graining of a Cellular Automaton

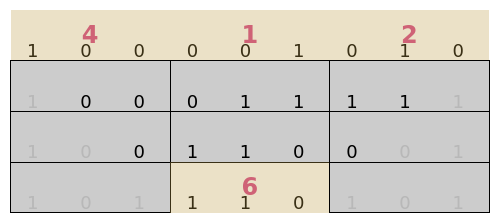
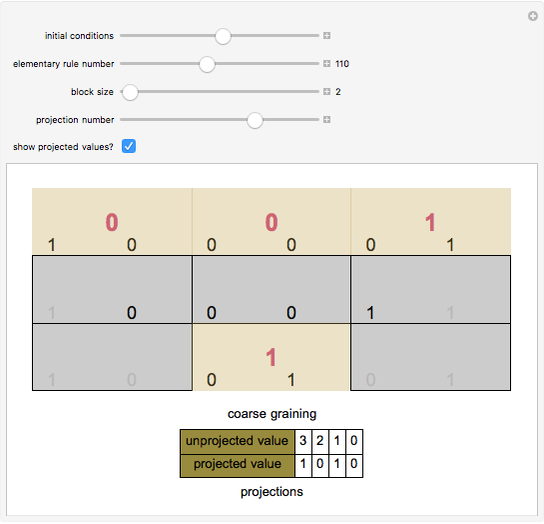
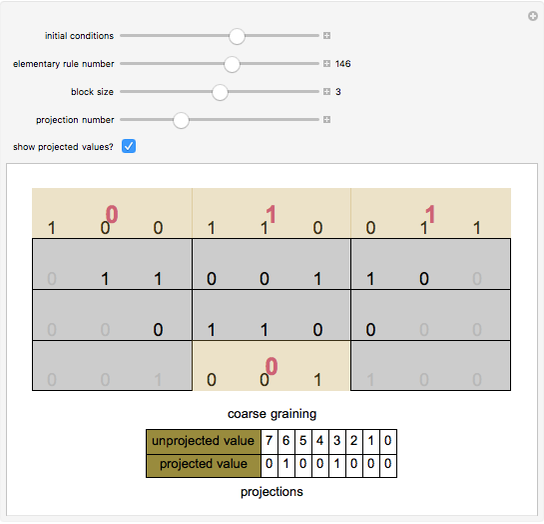
You can "coarse-grain" an elementary cellular automaton by creating blocks of length and running the cellular automaton for steps. You then examine the base 2 value of each initial run of 3 blocks and the base 2 value of the final block centered below each run. If you perform this task over all possible blocks of 3, you can develop an alternative characterization of the cellular automaton that has "colors." If you are willing to accept a loss of information, however, you can project the colors back into two colors. For most such projections, the result will not itself describe a cellular automaton because the same projected values will often have different outputs. Under certain projections, however, the result will describe a cellular automaton that is a "lossy" version of the original. This Demonstration helps visualize this idea by permitting you to select initial conditions, the elementary cellular automaton that is to be studied, a block size ranging from 2 to 4, and which of the projections should be examined. It creates a single run of 3 blocks and shows the evolution of the cellular automaton and the values (projected or not) of the initial 3 blocks and the final block.