Creep and Stress Relaxation for Four-Element Viscoelastic Solids and Liquids

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
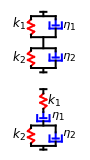
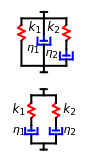
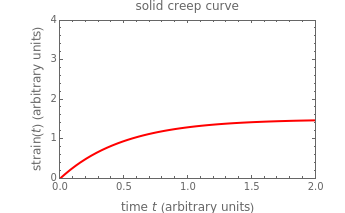
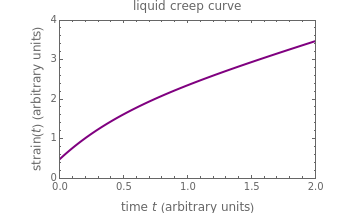
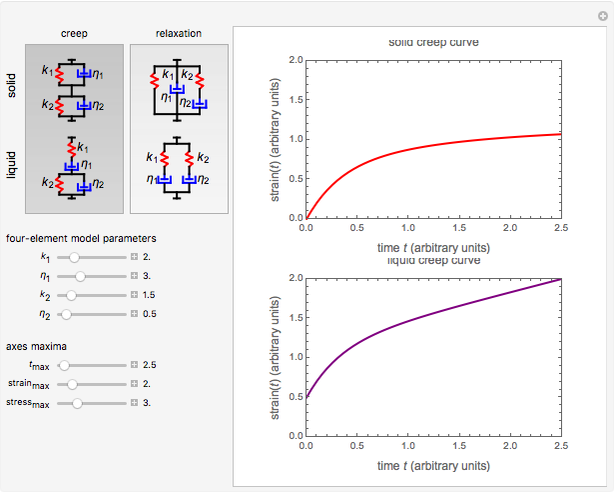
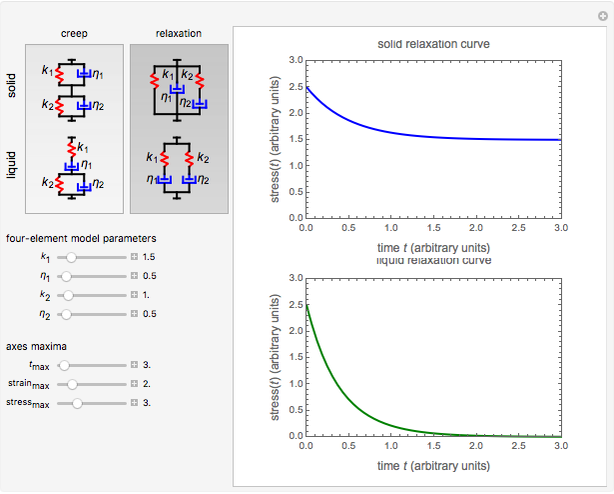
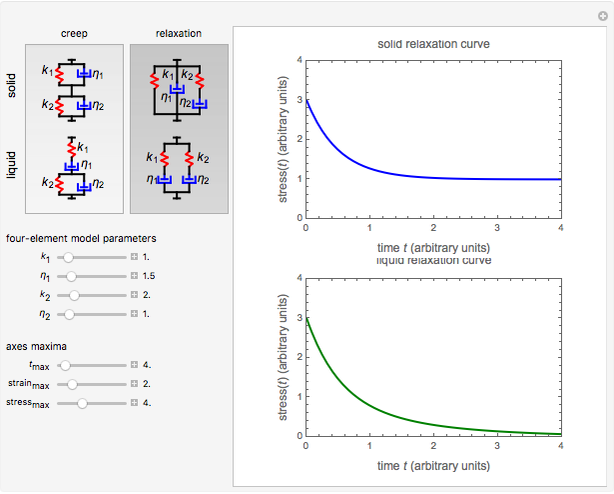
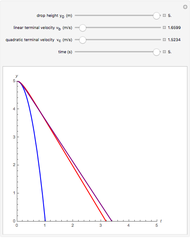
This Demonstration plots the creep curve under unit stress and the stress relaxation curve at constant unit strain of four-element solid and liquid mechanical analogs composed of two springs and two dashpots in different arrangements. For creep, the solid viscoelastic model is composed of two Kelvin–Voigt elements in series, and the liquid model is composed of a Maxwell and a Kelvin–Voigt element in series (the Burgers model). For relaxation, the solid model is composed of a Kelvin–Voigt and a Maxwell element in parallel, and the liquid model is composed of two Maxwell elements in series. Qualitatively, the generated creep and relaxation curves are similar to those of other four-element solid and liquid models. They show that the solid has asymptotic strain in creep and asymptotic residual stress in relaxation, while the liquid deforms indefinitely in creep and asymptotically reaches zero residual stress in relaxation.
Contributed by: Mark D. Normand and Micha Peleg (April 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: creep curve under unit stress with 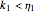 and
and 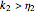
Snapshot 2: stress relaxation curve at unit strain with 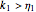 and
and 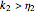
Snapshot 3: stress relaxation curve at unit strain with 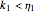 and
and 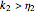
A four-element mechanical analog is one of eight different ("nondegenerate") arrangements of two springs and two dashpots. It behaves like a viscoelastic solid if the arrangement cannot be separated because of one or two springs in series, and like a viscoelastic liquid if the arrangement can be separated into two parts by the disengagement of one or two dashpots. For convenience, the solid model is presented as two Kelvin–Voigt elements in series for creep, and as a Kelvin–Voigt and a Maxwell element in parallel for stress relaxation. The liquid model is presented as a Kelvin–Voigt and a Maxwell element in series for creep, and as two Maxwell elements in parallel for relaxation. The corresponding creep curve equations are: 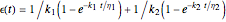 for the solid and
for the solid and  for the liquid model, and for the stress relaxation,
for the liquid model, and for the stress relaxation, 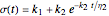 for the solid and
for the solid and 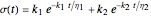 for the liquid models, respectively, where
for the liquid models, respectively, where 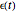 is the strain,
is the strain, 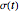 is the stress,
is the stress, 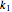 and
and 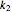 are the spring constants in arbitrary stress units, and
are the spring constants in arbitrary stress units, and 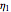 and
and 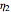 are the dashpots' viscosities in units of arbitrary stress × time [1, 2].
are the dashpots' viscosities in units of arbitrary stress × time [1, 2].
In this Demonstration, you can choose the plot type, creep, or stress relaxation by clicking the corresponding setter bar, and you can select the magnitudes of 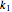 ,
, 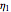 ,
, 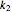 , and
, and 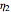 with sliders. The program calculates and plots the corresponding curves for the viscoelastic solid and liquid. You can also vary the time and maxima of the plots for the strain and stress axes for improved resolution.
with sliders. The program calculates and plots the corresponding curves for the viscoelastic solid and liquid. You can also vary the time and maxima of the plots for the strain and stress axes for improved resolution.
References
[1] D. R. Bland, The Theory of Linear Viscoelasticity, New York: Pergamon Press, 1960.
[2] W. N. Findley, J. S. Lai, and K. Onaran, Creep and Relaxation of Nonlinear Viscoelastic Materials, New York: North-Holland Publishing Company, 1976.
Permanent Citation