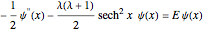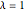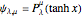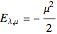Eigenstates for Pöschl-Teller Potentials

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
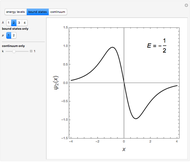
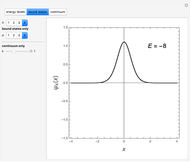
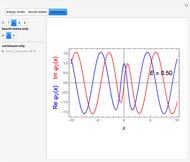
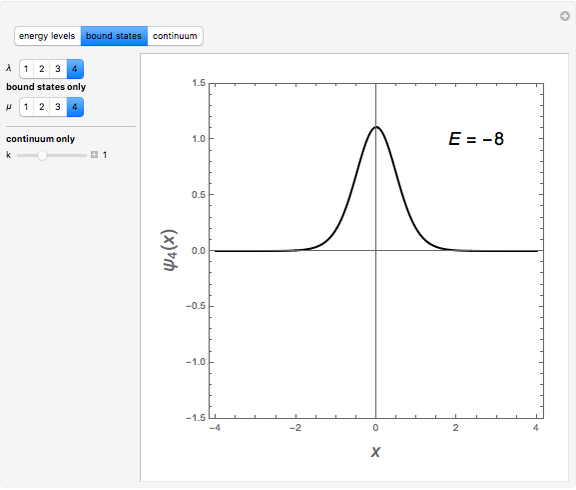
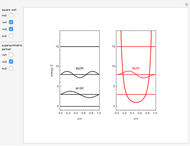
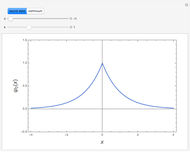
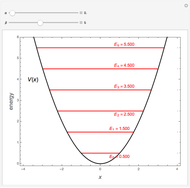
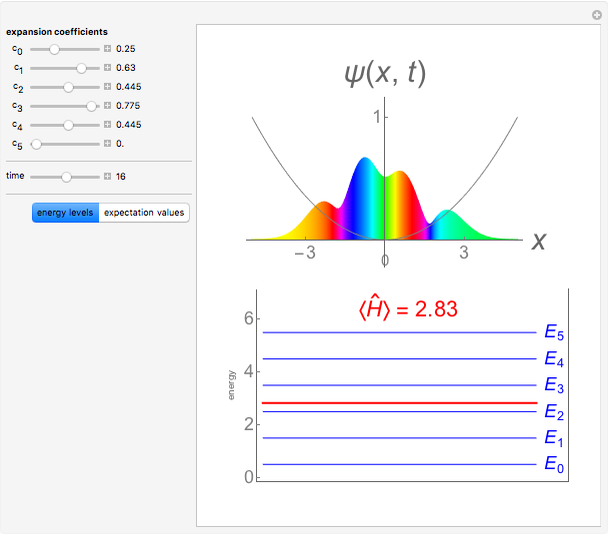
It has been long known that the Schrödinger equation for a class of potentials of the form 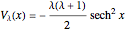 , usually referred to as Pöschl–Teller potentials, is exactly solvable. The eigenvalue problem
, usually referred to as Pöschl–Teller potentials, is exactly solvable. The eigenvalue problem
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
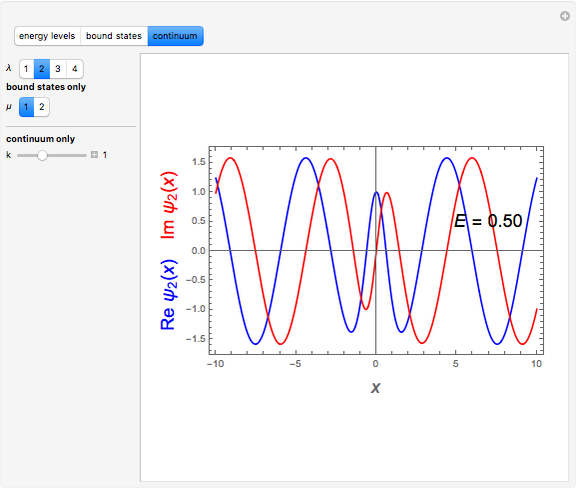
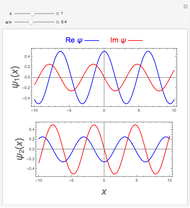
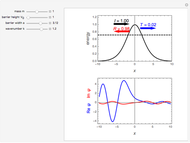
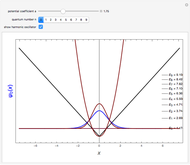
Snapshots
Details
References:
G. Pöschl and E. Teller, "Bemerkungen zur Quantenmechanik des Anharmonischen Oszillators", Z. Phys., 83(3,4), 1933 pp. 143–151.
A recent discussion of reflectionless scattering is given by J. Lekner, "Reflectionless Eigenstates of the  Potential," American Journal of Physics, 75(12), 2007 pp. 1151–1157.
Potential," American Journal of Physics, 75(12), 2007 pp. 1151–1157.
Permanent Citation