Details

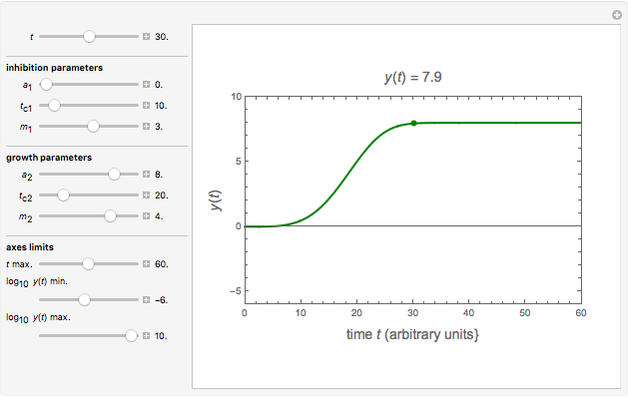
Snapshot 1: pure growth

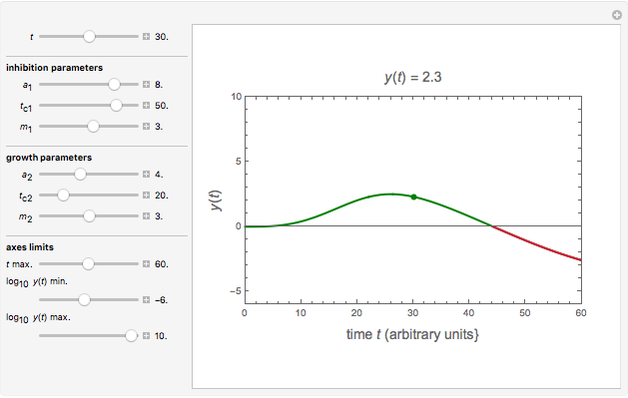
Snapshot 2: suppressed growth followed by inactivation

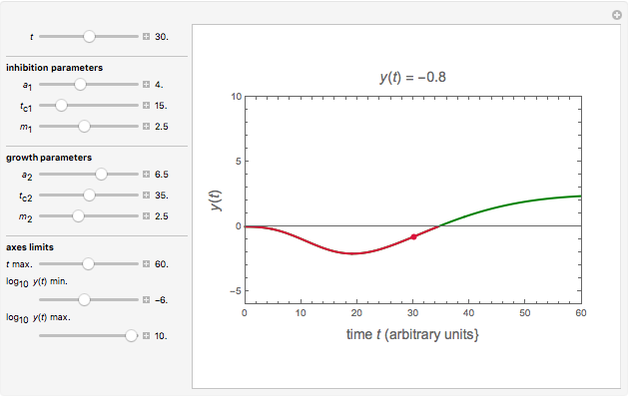
Snapshot 3: incomplete inactivation followed by suppressed growth

Snapshot 4: pure inactivation

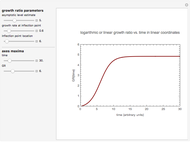
A microbial population in a nutritious medium such as food tends to grow through cell division. A typical sigmoid growth curve of a microbe in a closed habitat is a reflection of four phases: a lag phase where the population's size remains small and unchanged, followed by an exponential growth phase that turns into a stationary phase, after which decline and mortality ensue. Almost always, only the first two or three phases are of consequence to food safety and stability. An introduced chemical antimicrobial can affect the cycle in different ways, qualitatively and quantitatively. Depending on its concentration and other conditions, the antimicrobial agent can be lethal from the start, turning the growth curve into an inactivation (survival) curve, or it can retard the exponential growth phase, suppress the overall growth level, lower the growth rate, or any combination of those. These growth/inactivation patterns suggest that the momentary population size is determined by a changing balance between two conflicting mechanisms: the agent's deleterious activity and the organism's attempt to survive and grow.

This can be described mathematically, at least qualitatively, by the following argument. Define the growth/inactivation state by the linear or logarithmic ratios or , respectively, where is the initial and is the momentary number of cells. At , . Net growth is manifested when and inactivation when . We can express this ratio's time dependence by the double stretched exponential model , where the first term represents the lethal/suppressive effect and the second term represents the cell's tendency to divide. The are scale factors, the are the two mechanisms' characteristic times, and the are shape factors that you can enter and vary with sliders.

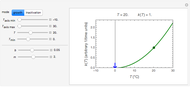
Using the six parameters' values and also those of the axes maxima, the corresponding curve is plotted. It is green when is positive and red when negative. The numerical momentary value of , marked as a moving dot on the curve controlled by the slider, is displayed above the plot.