Stochastic Model of Microbial Injury and Mortality

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
During microbial inactivation, especially under marginal or sub-lethal conditions, cells or spores of the targeted organism can exist in one of three states: dead (fully inactivated), injured, or intact, with corresponding time-dependent probabilities. In this Demonstration, the process is simulated starting with a chosen number of intact cells or spores, generating their Markov trees, recording their state after time increments, and displaying the results. The survival and injury curves so produced let you compare the stochastic behavior of small cell or spore populations and almost fully deterministic behavior of large populations. The curves can also be used to examine how the varying probabilities of each state affect the survival and injury patterns.
Contributed by: Mark D. Normand , Maria G. Corradini, and Micha Peleg (September 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: survival curve of a small ( ) population
) population
Snapshot 2: survival curve of another small (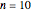 ) population
) population
Snapshot 3: injury curve of a small (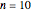 ) population
) population
Snapshot 4: injury curve of another small (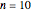 ) population
) population
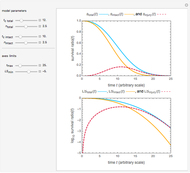
Snapshot 5: the number of intact cells in a large (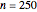 ) population
) population
Snapshot 6: the number of injured cells in a large (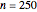 ) population
) population
Snapshot 7: the survival curve of a large (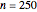 ) population
) population
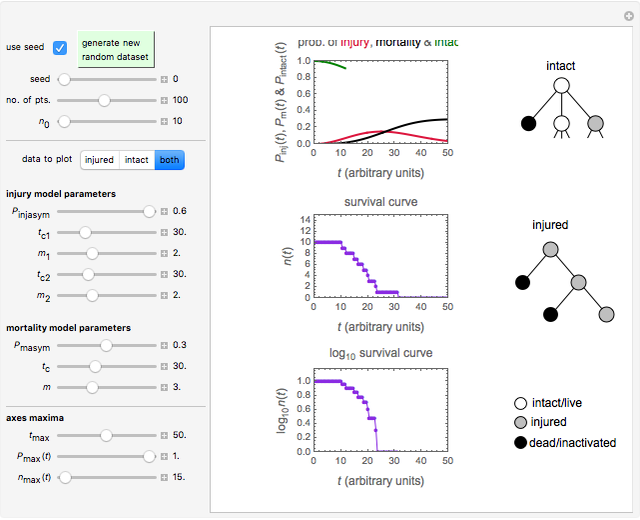
Using a stochastic model, this Demonstration simulates the mortality, injury, and intact-survival patterns of a microbial population exposed to a hostile environment or lethal agent, such as thermal processing, ultra-high hydrostatic pressure, or chemical disinfection [1, 2]. The starting point is a chosen initial number of intact cells or spores 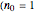 to
to  at
at  ). After a unit time increment
). After a unit time increment  there is a probability
there is a probability  that each individual microbe will be dead or fully inactivated,
that each individual microbe will be dead or fully inactivated, 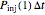 that it will be injured, and
that it will be injured, and 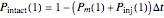 that it will remain intact, where
that it will remain intact, where 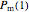 ,
, 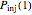 , and
, and 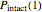 are the values of the corresponding probability rate functions. If the microbe, vegetative cell, or spore survived the first round intact, then after another time increment
are the values of the corresponding probability rate functions. If the microbe, vegetative cell, or spore survived the first round intact, then after another time increment  , it will have a probability of
, it will have a probability of 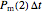 that it will die or be inactivated,
that it will die or be inactivated, 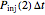 that it will be injured, and
that it will be injured, and 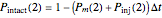 that it will still remain intact. If the microbe were injured in round 1, there is a probability
that it will still remain intact. If the microbe were injured in round 1, there is a probability 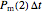 that the microbe will die or be inactivated, and a probability
that the microbe will die or be inactivated, and a probability 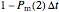 that it remains injured. The schematic diagram to the right of the plots shows the possible states of an intact or injured cell or spore. The process is iterated (
that it remains injured. The schematic diagram to the right of the plots shows the possible states of an intact or injured cell or spore. The process is iterated (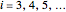 ) until the microbe dies off or the maximum assigned number of iterations is reached. The procedure is repeated with each of the
) until the microbe dies off or the maximum assigned number of iterations is reached. The procedure is repeated with each of the  individual microbes. The temporary number of microbes at each state (after each iteration) is recorded. The "data to plot" setter is used to select which bottom two plots are visible, that is, those of the injured microbes, intact microbes, or both.
individual microbes. The temporary number of microbes at each state (after each iteration) is recorded. The "data to plot" setter is used to select which bottom two plots are visible, that is, those of the injured microbes, intact microbes, or both.
The equations used to calculate and display the probability rate functions are 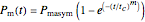 ,
, 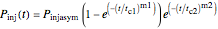 , and
, and 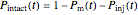 . In these equations the
. In these equations the 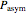 's are the upper asymptotic levels of the three probability rate functions, the
's are the upper asymptotic levels of the three probability rate functions, the 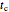 's are characteristic times and the
's are characteristic times and the  's are shape factors controlling the steepness of the terms around their inflection points. These variables are entered with sliders. Also entered with sliders are the initial number of intact cells or spores,
's are shape factors controlling the steepness of the terms around their inflection points. These variables are entered with sliders. Also entered with sliders are the initial number of intact cells or spores,  , the seed of the random number generator and the number of data points (iterations or
, the seed of the random number generator and the number of data points (iterations or  increments) and the plots' axes maxima.
increments) and the plots' axes maxima.
The top plot displays the three probability rate functions. The chosen injury curve, intact number curve, or traditional survival curve, constructed as their sum, are displayed on linear and semilogarithmic coordinates in the middle and bottom plots, respectively. Notice that the 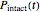 curve is truncated at the point where there are no remaining intact cells or spores. Also note that not all the allowed parameter combinations necessarily have a corresponding real microbial population.
curve is truncated at the point where there are no remaining intact cells or spores. Also note that not all the allowed parameter combinations necessarily have a corresponding real microbial population.
The mathematical model used in this Demonstration does not take into account the degree of injury and that the probability rate functions could be not only functions of time but could also vary within the branches of the Markov tree. Despite these oversimplifications, the model provides a realistic view of the changing roles of mortality and injury and of the differences in the responses of small and large microbial populations to a hostile environment.
References
[1] V. C. H. Wu, "A Review of Microbial Injury and Recovery Methods in Foods," Food Microbiology, 25, 2008 pp. 735–744.
[2] M. G. Corradini and M. Peleg, "A Weibullian Model of Microbial Injury and Mortality," International Journal of Food Microbiology, 119(3), 2007 pp. 319–328. doi:10.1016/j.ijfoodmicro.2007.08.035.
Permanent Citation