Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Fisher Discriminant Analysis

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

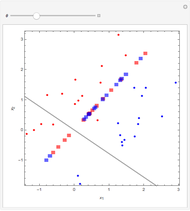
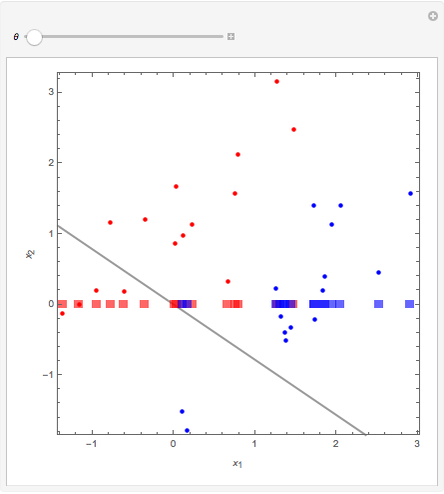
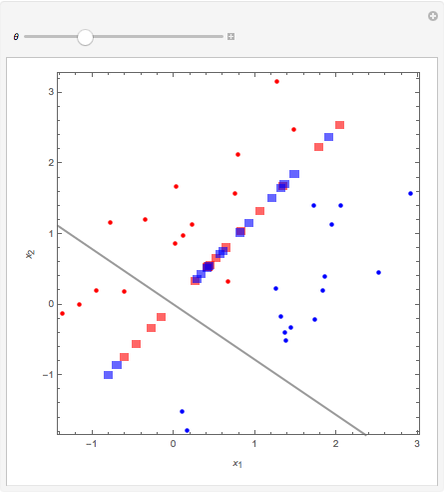
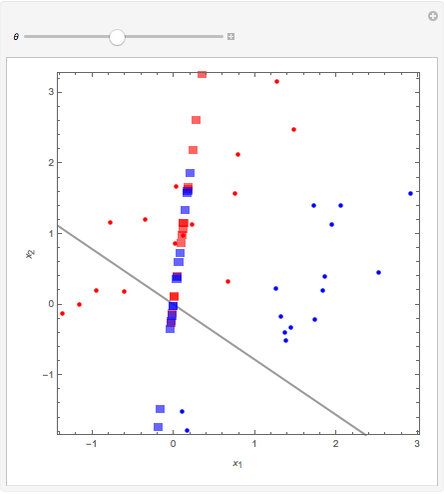
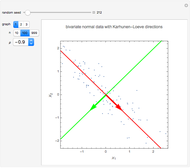
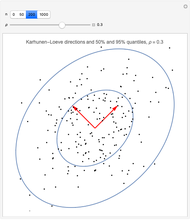
The 30 round points are data. The 15 red points were generated from a normal distribution with mean , the 15 blue ones with mean , and in both cases the covariance matrix was the identity matrix. The problem is to classify or predict the color using the inputs and .

[more]

Fisher linear discriminant analysis determines a canonical direction for which the data is most separated when projected on a line in this direction. The solid gray line shows the canonical direction.

The squares are projected points on a line inclined at the angle with respect to the origin. When is adjusted so the projected points are aligned with the gray line, the points are maximally separated in the sense that the ratio of between-classes variances to within-classes variance is maximized.

A point is predicted as red or blue according to whether its projection on the canonical direction lies closest to the projected mean of the red or blue data points.

[less]

Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The canonical direction is given by

,

where and are the between- and within-classes covariance matrices. Hastie, Tibshirani and Friedman (2009, §4.3.3) [3] show that is given by the largest eigenvalue of .

The more general case where the number of inputs is greater than 2 is also considered in [3], but the basic principle of finding the canonical direction is the same. In our illustrative problem we have inputs as well as classes. In general, there are orthogonal canonical directions with the first canonical direction as defined above. Sometimes, as in [2], it is sufficient just to use just the first canonical component. For extensions, see [3].

[1] Wikipedia, "Linear Discriminant Analysis."

[2] R. A. Fisher, "The Use of Multiple Measurements in Taxonomic Problems," Annals of Eugenics, 7, 1936 pp. 179–188.

[3] T. Hastie, R. Tibshirani, and J. Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed., New York: Springer, 2009.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send