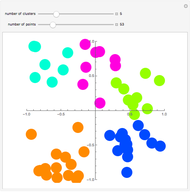
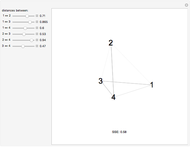
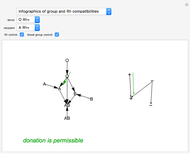
Loading Plot of a Principal Component Analysis (PCA)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
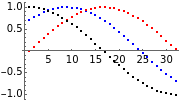
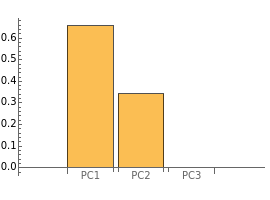
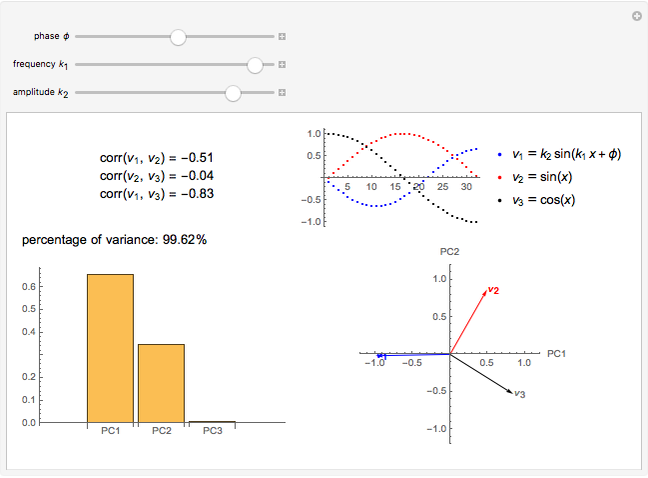
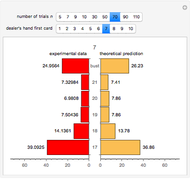
Principal component analysis (PCA) is a statistical procedure that converts data with possibly correlated variables into a set of linearly uncorrelated variables, analogous to a principal-axis transformation in mechanics.
[more]
Contributed by: D. Meliga and S. Z. Lavagnino (May 2016)
With additional contributions by: A. Chiavassaand M. Aria
Open content licensed under CC BY-NC-SA
Snapshots
Details
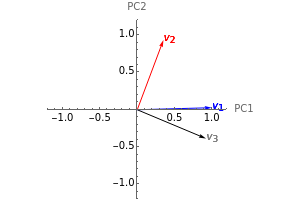
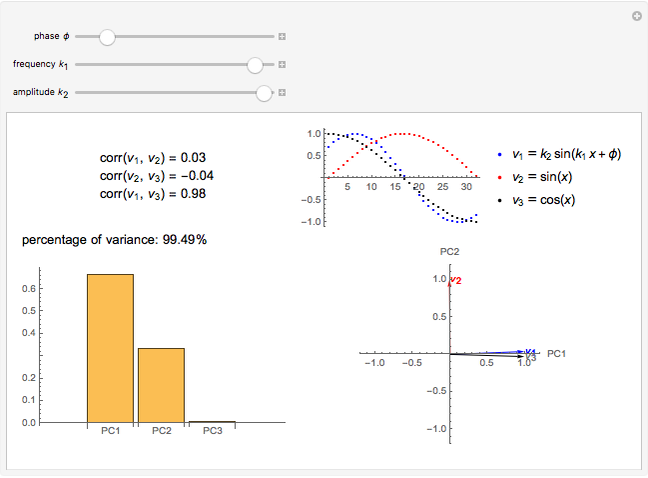
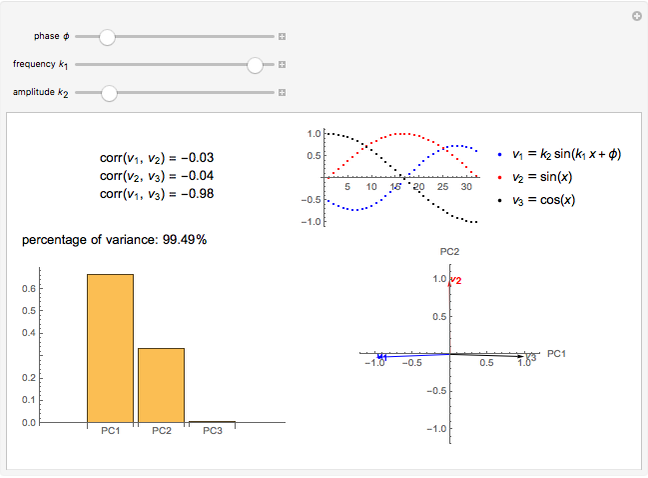
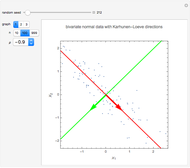
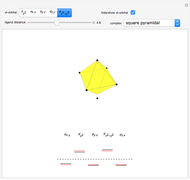
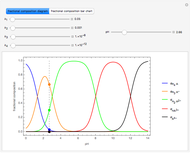
In the loading plot, the high correlation between two variables leads to two vectors that are very close to each other, the non-correlation leads to two vectors out of phase by 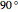 , while the anti-correlation leads to two vectors that are out of phase by
, while the anti-correlation leads to two vectors that are out of phase by 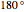 [2].
[2].
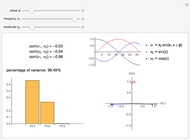
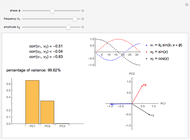
Snapshot 1: a strong correlation between 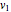 and
and 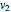
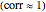 , non-correlation in the remaining cases
, non-correlation in the remaining cases 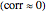 . From a graphical point of view, we can see two vectors that are very close, while the others are out of phase with each other by about
. From a graphical point of view, we can see two vectors that are very close, while the others are out of phase with each other by about 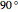 .
.
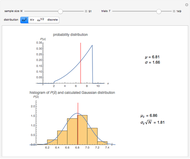
Snapshot 2: a strong correlation between 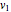 and
and 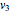
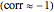 , non-correlation in the remaining cases
, non-correlation in the remaining cases 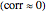 . From a graphical point of view, we can see two opposite vectors, while the others are out of phase to each other by about
. From a graphical point of view, we can see two opposite vectors, while the others are out of phase to each other by about 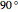 .
.
References
[1] S. J. Press, Applied Multivariate Analysis: Using Bayesian and Frequentist Methods of Inference, Mineola, NY: Dover Publications, 2005.
[2] M. Aria. "L'analisi in Componenti Principali." (May 25, 2016) www.federica.unina.it/economia/analisi-statistica-sociologica/analisi-componenti-principali.
Permanent Citation