Wolfram Demonstrations Project

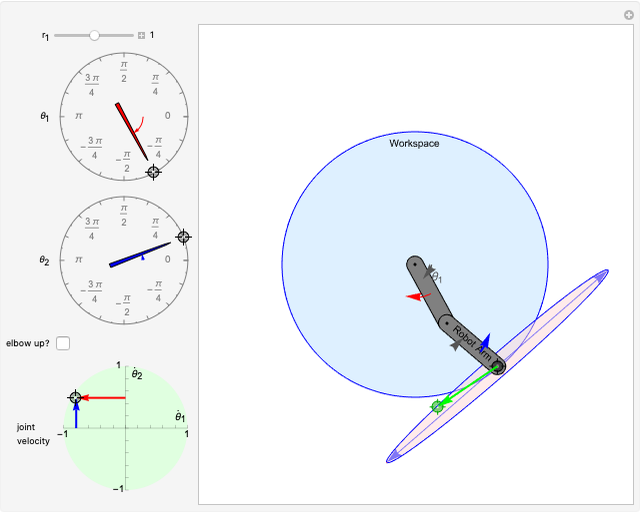
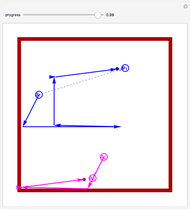
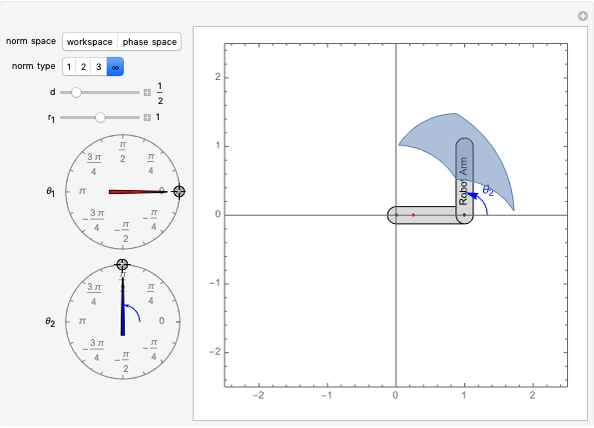
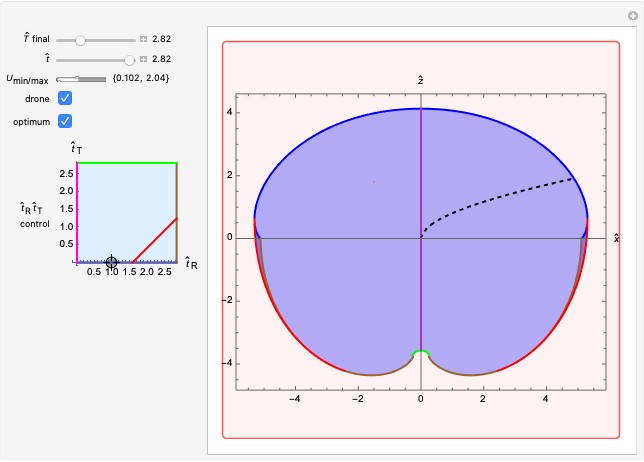
This Demonstration lets you control a two-link revolute-revolute robot arm either by setting the two joint angles (this is called forward kinematics) or by dragging a locator specifying the tip of the end effector (this is called inverse kinematics). Most locations in the workspace have two solutions to the inverse kinematics and can be selected with the "elbow up?" check box. The joint velocities are limited to magnitudes less than or equal to 1, represented by a green disc. Joint velocities map to a velocity of the end effector, drawn with a green locator (this is called forward velocity kinematics). Dragging the green locator maps to joint velocities (this is called inverse velocity kinematics). You can vary the relative link lengths under the constraint that

Contributed by: Aaron T. Becker and Lillian Lin

Drag Locators
Slider Zoom
Gamepad Controls
Automatic Animation

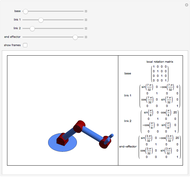
A robot arm, or robot manipulator, is constructed from two types of joints, prismatic and revolute. A revolute joint rotates on a single plane along an axis centered at the joint, while a prismatic joint moves linearly, extending along a line. The transformation from joint angles to the location of the end effector is called forward kinematics and can be computed by a series of matrix multiplications.

Each joint transforms the coordinate frame from the previous joint. These coordinate transformations are multiplied together to determine the location of the end effector. The Denavit–Hartenberg convention represents the transformation due to the

joint as [1]:

, where

and

A sequence of matrices

are then multiplied together to give the location of the end effector.

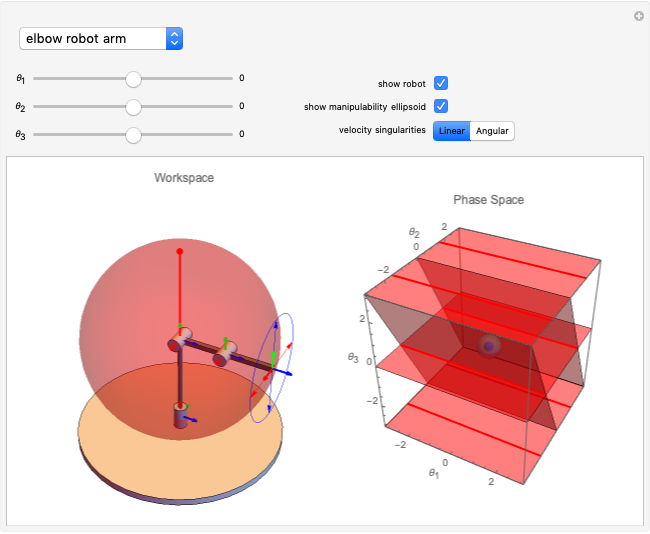
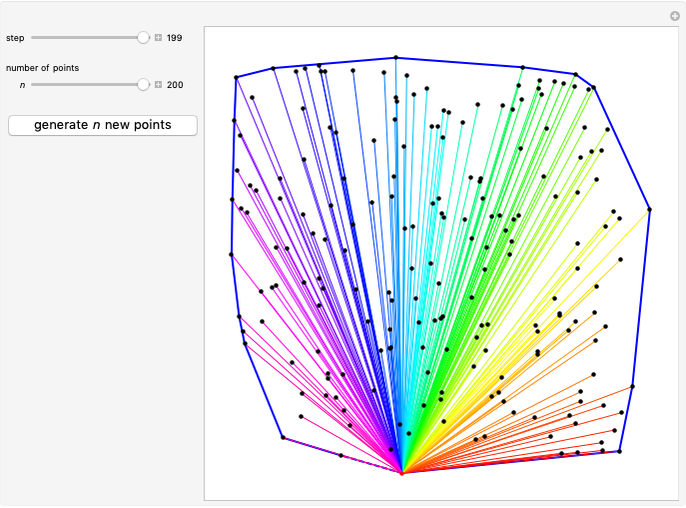
The transformation from the end effector location to joint angles is usually challenging because it often involves inverse trigonometric functions. Often there are multiple solutions, and the transformation is sometimes impossible (some end effectors are outside the workspace of the robot). Even for this simple two-link robot, these issues are present. The reachable workspace is drawn in blue. All locations outside of this region are impossible to reach. All locations on the boundary of this workspace have only one solution, but locations inside the blue region can be reached by two configurations, called the "elbow up" and "elbow down" configurations.

The transformation from joint velocities

to end effector velocities

is called forward velocity kinematics. It can be computed by taking the derivative of the forward kinematics equations and multiplying this by the joint velocities. This gives the Jacobian, a function of the current robot configuration and is represented by

, where

is a vector of joint angles:

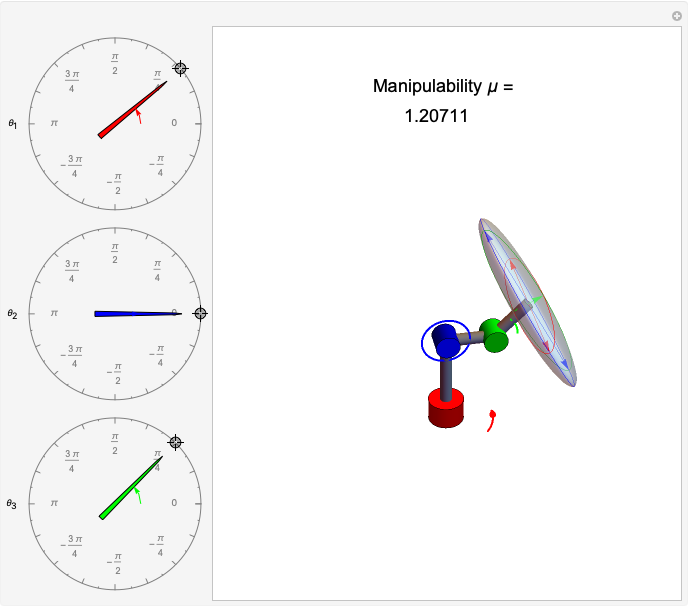
If all joint velocities are within the unit ball

, then the end effector velocities are constrained to lie within an ellipse, drawn in pink in the figure. This ellipse is called the manipulability ellipse.

The inverse problem of determining what joint velocities

are required to generate a desired

is inverse velocity kinematics. Inverse velocity kinematics is trivial if

exists:

, but when

is singular this is not possible. In this Demonstration, singular configurations occur on the boundary of the workspace, where the manipulability ellipse loses a dimension and becomes a line. In this case, we solve for the required joint velocities by generating the Moore–Penrose pseudoinverse. This is calculated in Mathematica as PseudoInverse[J]·ξ= q'.

Reference

[1] M. W. Spong, S. Hutchinson, and M. Vidyasagar, Robot Modeling and Control, Hoboken, NJ: John Wiley and Sons, 2006.