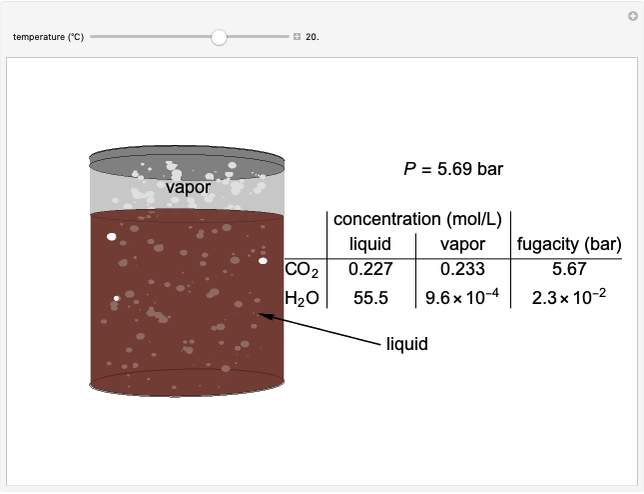
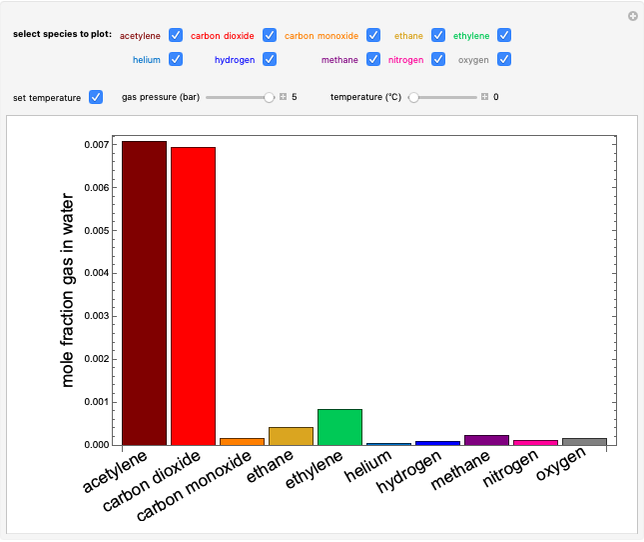
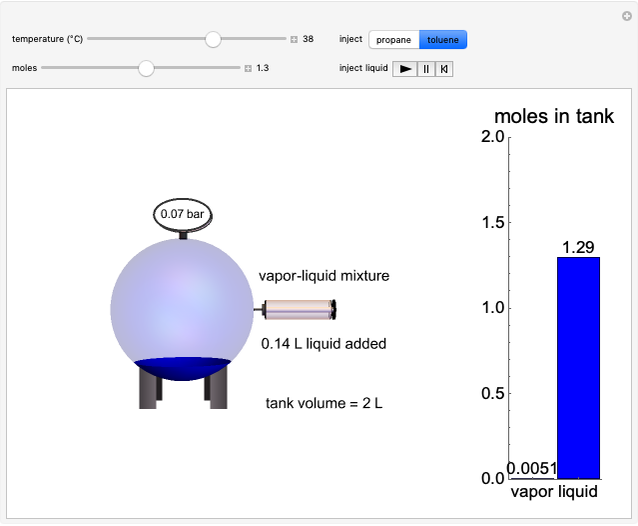
The fugacities of water and carbon dioxide are calculated as a function of temperature for a closed container, which is a model of a can of soda. The concentrations of the two components are calculated in both the liquid and gas phases. As temperature increases, the pressure increases, and therefore the fugacities increase. Note that the concentration is much lower than the concentration in the liquid phase, but the concentration is much higher than the concentration in the gas phase. Because the gas phase is assumed to be ideal, the fugacities of and in both phases are equal to their gas-phase partial pressures, and thus the fugacity is much higher than the fugacity. As the temperature increases, the concentration in liquid water decreases. However, as the temperature increases the pressure increases, and a higher pressure increases the concentration in water, so the net effect is that concentration in the liquid phase does not change much as the temperature increases.