Kepler and Oscillator Elliptical Orbits

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
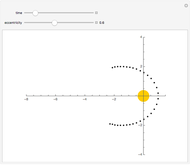
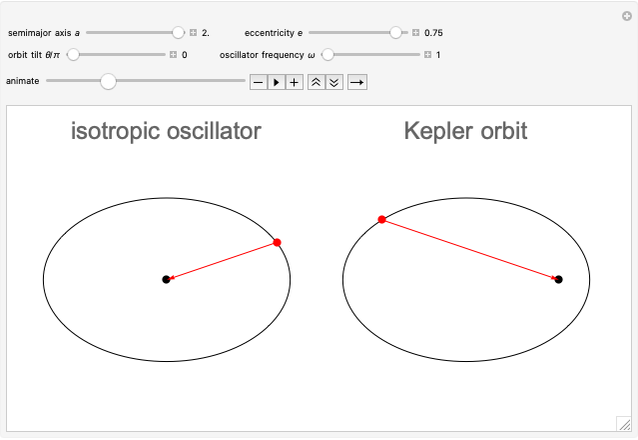
According to Bertrand's theorem, the only central forces that result in closed orbits for all bound particles, independent of initial conditions, are the inverse-square law or Hooke's law. The corresponding central forces are proportional to  or
or  , associated with the Kepler problem or the isotropic two-dimensional oscillator, respectively. Isaac Newton recognized in the Principia [1] that both problems could admit elliptical orbits. For the oscillator, the center of force is at the center of the ellipse, while for the Kepler problem, it is at one focus of the ellipse.
, associated with the Kepler problem or the isotropic two-dimensional oscillator, respectively. Isaac Newton recognized in the Principia [1] that both problems could admit elliptical orbits. For the oscillator, the center of force is at the center of the ellipse, while for the Kepler problem, it is at one focus of the ellipse.
Contributed by: S. M. Blinder (January 2021)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The motion of the oscillator is given by
 ,
,
 .
.
An elliptical Kepler orbit can be represented in polar coordinates by
 ,
,
where the energy  and angular momentum
and angular momentum  of the orbit are given by
of the orbit are given by
 ,
,
 .
.
Here  is the mass of the center of force,
is the mass of the center of force,  the mass of the orbiting body and
the mass of the orbiting body and  the gravitational constant. It is assumed that
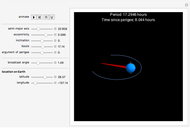
the gravitational constant. It is assumed that  (otherwise reduced mass must be introduced). The period of the orbit is given by Kepler's third law:
(otherwise reduced mass must be introduced). The period of the orbit is given by Kepler's third law:
 .
.
For simplicity, assume units such that  .
.
The mean anomaly  (not to be confused with the mass above) is the hypothetical angle about the center of the Kepler ellipse assuming uniform motion. Thus
(not to be confused with the mass above) is the hypothetical angle about the center of the Kepler ellipse assuming uniform motion. Thus
 .
.
The actual motion is described by the eccentric anomaly  , related to
, related to  by Kepler's equation
by Kepler's equation
 .
.
The equation is transcendental, but an accurate solution for  in the form of a Fourier sine series can be derived [2]:
in the form of a Fourier sine series can be derived [2]:
 .
.
References
[1] S. Chandrasekhar, Newton's Principia for the Common Reader, Oxford: Clarendon Press, 1995 pp. 114–125.
[2] M. A. Murison. "Series Solutions of Kepler's Equation." (Nov 30, 2020) www.murison.alpheratz.net/Maple/KeplerSolve/KeplerSolve.pdf.
Permanent Citation