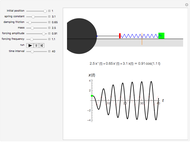
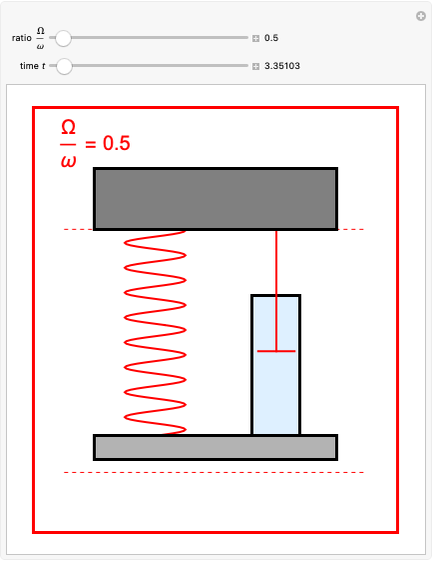
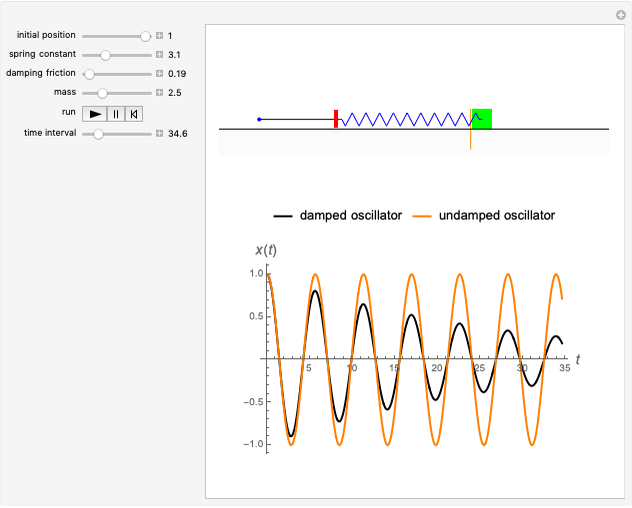
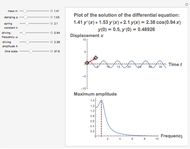
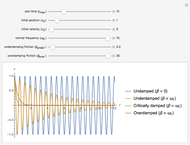
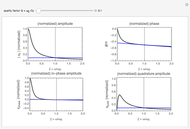
Oscillator with Generalized Power-Law Damping

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The standard problem of a linear oscillator with linear damping is represented by the well-known differential equation
[more]
Contributed by: S. M. Blinder (January 2021)
Open content licensed under CC BY-NC-SA
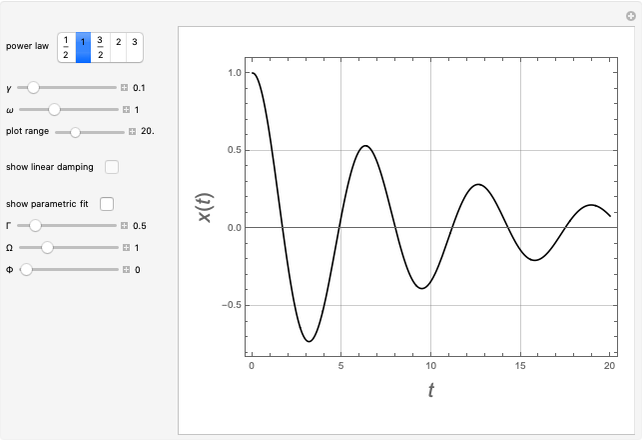
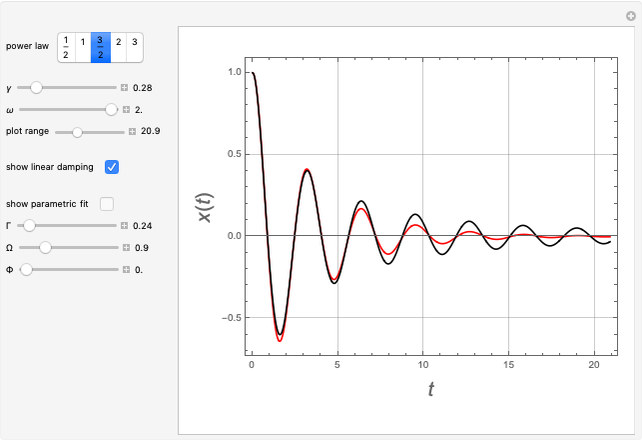
Snapshots
Details
Discussions of oscillator damping can be found in [1–3].
References
[1] J. L. Lancaster, "Slow-Dissipation Limit of the Harmonic Oscillator with General Power-Law Damping," American Journal of Physics, 88(12), 2020 pp. 1151–1155. doi:10.1119/10.0001794.
[2] X.-J. Wang, C. Schmitt and M. Payne, "Oscillations with Three Damping Effects," European Journal of Physics, 23(2), 2002 pp. 155–164.
[3] T. H. Fay, "Quadratic Damping," International Journal of Mathematical Education in Science and Technology, 43(6), 2012 pp. 789–803. doi:10.1080/0020739X.2011.622806.
Permanent Citation