Principal Stresses in Compacted Cohesive Powders

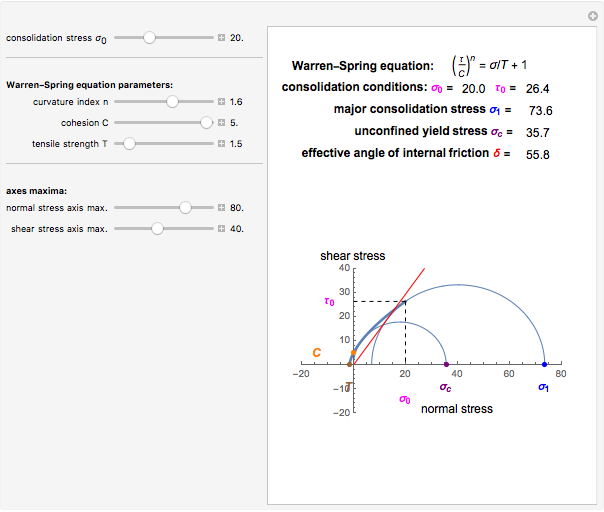
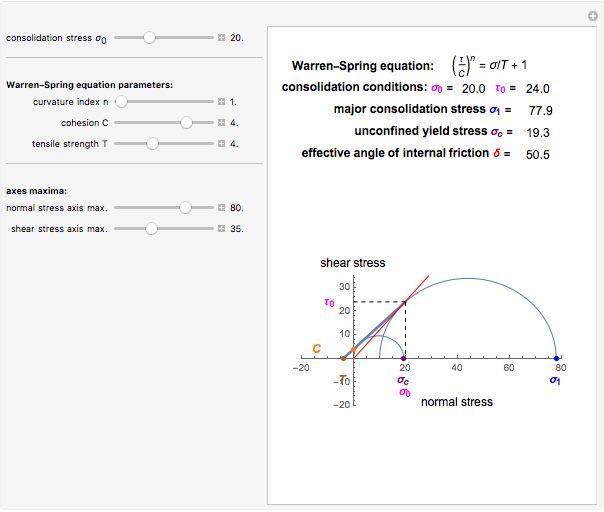
This Demonstration helps to visualize the effects of the Warren–Spring equation parameters and consolidation conditions on the shape of the yield loci curve and a powder compact's strength. It can also be used to assess the flowability of cohesive powders from experimentally determined shear parameters. It finds and plots the Mohr semicircles that are tangential to the generated yield loci curve of a consolidated powder. 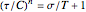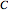The yield loci curve is described by the Warren–Spring equation , where is the shear stress, the cohesion, a curvature index, the normal stress, and 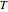the tensile strength. 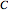The input parameters are the initial consolidation stress, and the Warren–Spring equation's coefficients, , , and 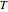, presumably obtained from experimental shear data by nonlinear regression. Their values are entered using sliders. This Demonstration solves three pairs of simultaneous equations to find the unconfined yield stress 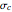, the major consolidation stress 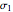, and the slope of the line tangent to the Mohr semicircle used to calculate 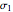, which defines the effective angle of internal friction. Their calculated values are displayed above a plot that depicts the yield loci curve, the two corresponding Mohr semicircles and the line used to find tan .

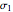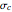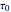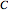, , , , , , and 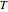are in stress units (e.g., kPa), is dimensionless, and is in degrees.

Note that not every possible plot produced by the demonstration corresponds to a real powder compact.

Snapshot 1: cohesive powder: yield loci curve with high degree of curvature and large angle of internal friction

Snapshot 2: cohesive powder: yield loci curve with low degree of curvature and small angle of internal friction

Snapshot 3: cohesive powder: linear yield loci curve and large angle of internal friction

Snapshot 4: "almost free-flowing" powder: almost linear yield loci curve and small angle of internal friction

References:

M. D. Ashton, R. Farely, and F. H. H. Valentin, "Some Investigations into the Strength and Flow Properties of Powders," Rheologica Acta, 4(3), 1965 pp. 206–218.

J. C. Williams, "The Storage and Flow of Powders," in M. J. Rhodes, ed., Principles of Powder Technology, New York: Wiley, 1990.

J. Schwedes, "Review on Testers for Measuring Flow Properties of Bulk Solids," Granular Matter, 5, 2003 pp. 1–43.