Projections of the Four-Cube

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
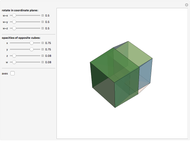
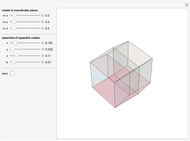
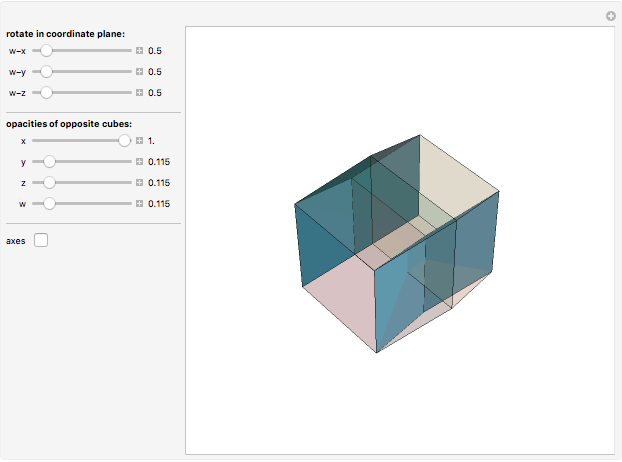
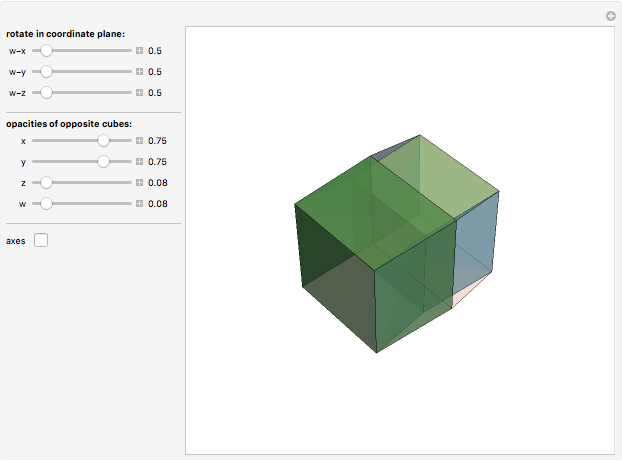
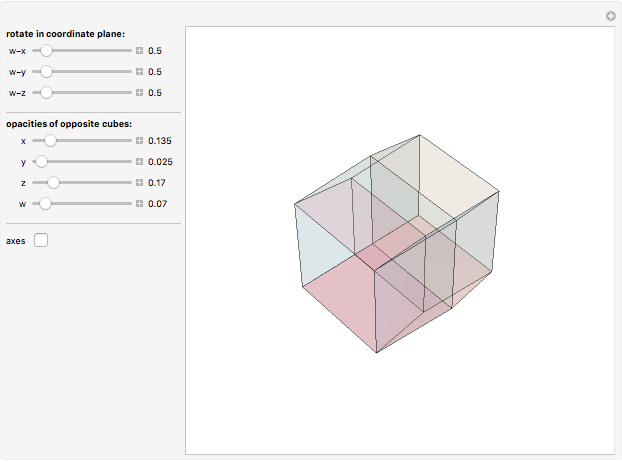
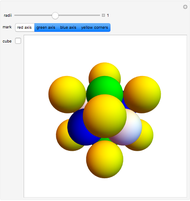
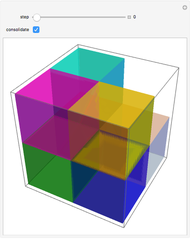
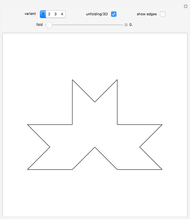
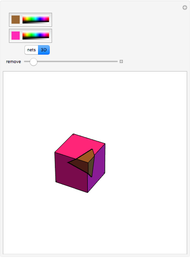
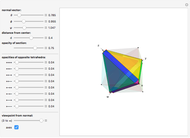
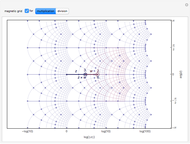
Rotate a four-dimensional cube and project it into three-dimensional graphics. The rotation is the composite of rotations in the w-x, w-y, and w-z planes, in that order. Opposite cubes (3-cells) of the hypercube have similar colors. Play with the opacity to see how the hypercube is bounded by eight cubes.
Contributed by: Michael Rogers (Oxford College/Emory University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
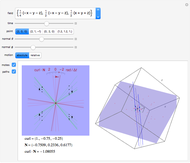
The rotation of the hypercube, whose vertices have coordinates each ±1, is the composite of rotations in the w-x, w-y, and w-z planes, in that order. Combined with Mathematica's built-in rotation of 3D graphics, this gives all six degrees of freedom of four-dimensional rotations. The bounding cubes are drawn in the order from least w coordinate to greatest. If all the opacities are set to one, the display shows the cubes "visible" looking from out on the positive w axis. The projection is accomplished by dropping the w coordinate; therefore it is a parallel projection, although the projection onto the screen has the default perspective of Mathematica 3D graphics. The positive x, y, z, w axes of the hypercube may be shown; these rotate with the hypercube, which helps illustrate how the rotations work.
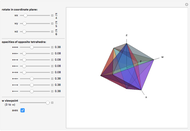
Snapshot 1: a pair of opposite cubes
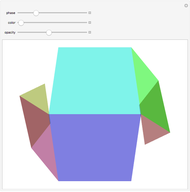
Snapshot 2: two pairs of opposite cubes
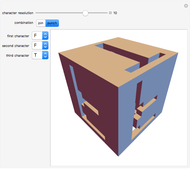
Snapshot 3: a variation on a classic projection of the hypercube
Permanent Citation
"Projections of the Four-Cube"
http://demonstrations.wolfram.com/ProjectionsOfTheFourCube/
Wolfram Demonstrations Project
Published: March 7 2011