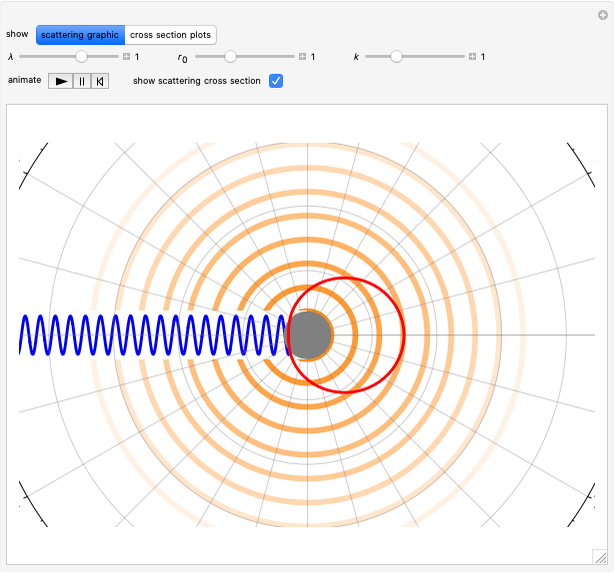
Scattering by a Dirac Bubble Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
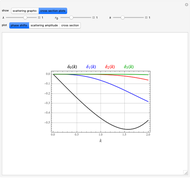
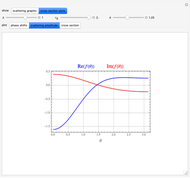
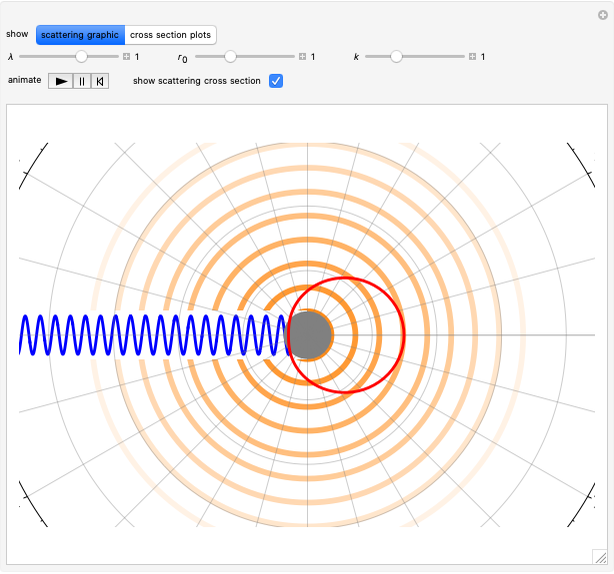
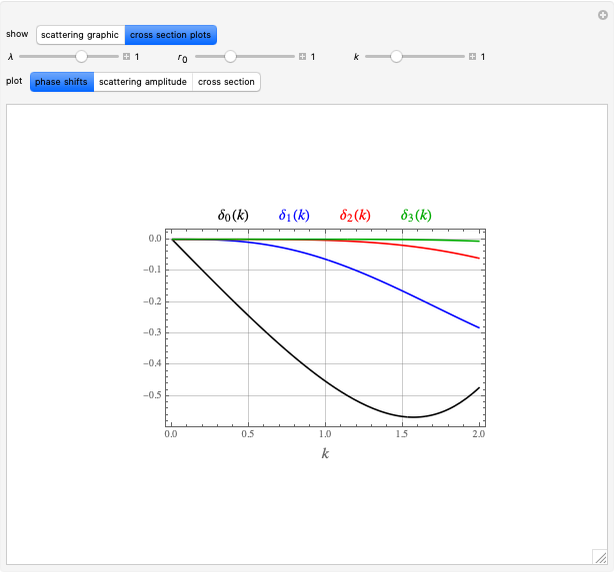
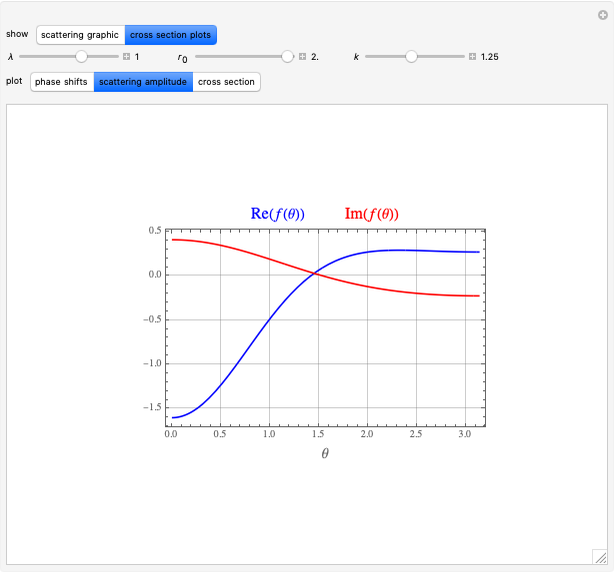
For elastic scattering from a spherically symmetrical potential, the asymptotic behavior of the wavefunction can be represented by the Faxen–Holzmark formula
[more]
Contributed by: S. M. Blinder (February 2021)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] S. M. Blinder, "Schrödinger Equation for a Dirac Bubble Potential," Chemical Physics Letters, 64(3), 1979 pp. 485–486. doi:10.1016/0009-2614(79)80227-4.
[2] L. D. Landau and E. M. Lifshitz, Quantum Mechanics: Non-relativistic Theory, 2nd ed. (J. B. Sykes and J. S. Bell, trans.), Oxford: Pergamon Press, 1965 Chapter XVII.
[3] E. Merzbacher, Quantum Mechanics, 3rd ed., New York: John Wiley & Sons, Inc., 1998 Chapter 13.
Permanent Citation