Simplified Model of Quantum Scattering

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
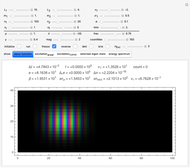
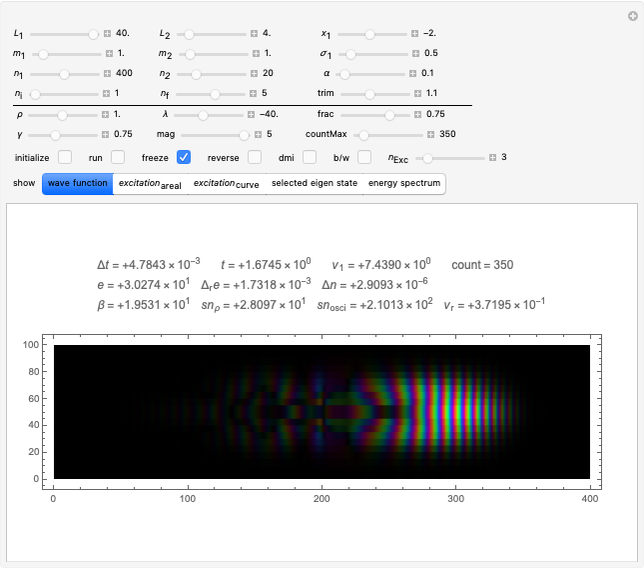
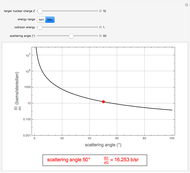
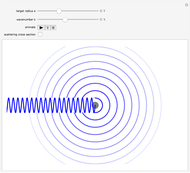
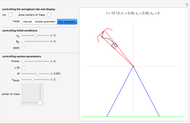
This Demonstration simulates the quantum dynamics of two interacting nonrelativistic particles. The goal is to demonstrate inelastic scattering in which a particle hits a target (a bound particle), excites the internal dynamics of the target and flies away with its state changed. The challenge is to arrange things in such a way that the essential features of inelastic scattering become visible in accessible observation times. We must make a considerable reduction in state-space dimension while conserving basic scattering geometry.
[more]
Contributed by: Ulrich Mutze (December 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
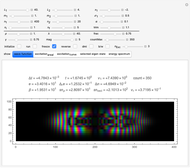
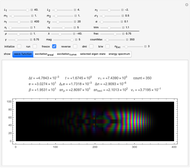
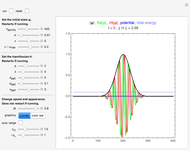
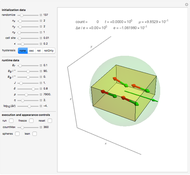
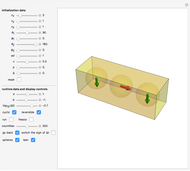
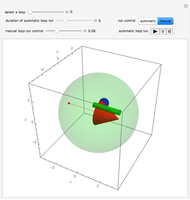
The following Snapshots all deal with the same system (the standard system in the bookmarks) for two values for the interacting coupling constant 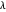 .
.
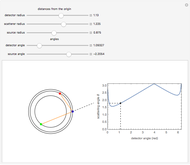
Snapshot 1: here we have 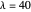 : strong repulsive interaction
: strong repulsive interaction
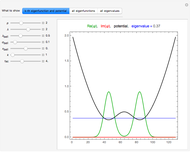
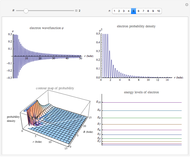
Snapshot 2: 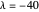 : strong attractive interaction
: strong attractive interaction
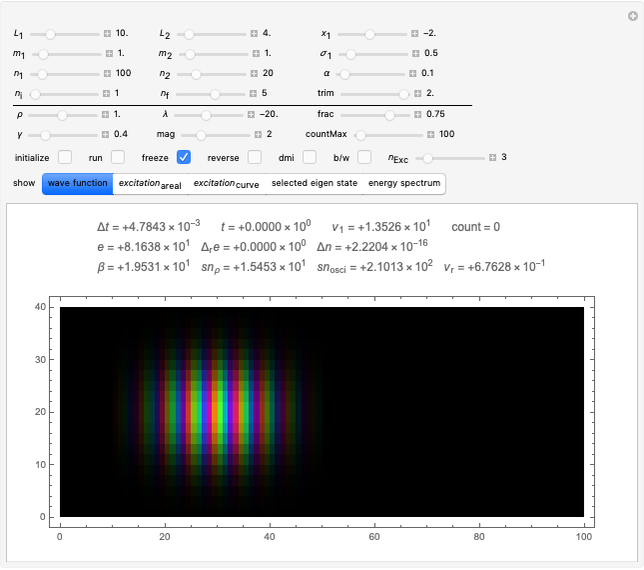
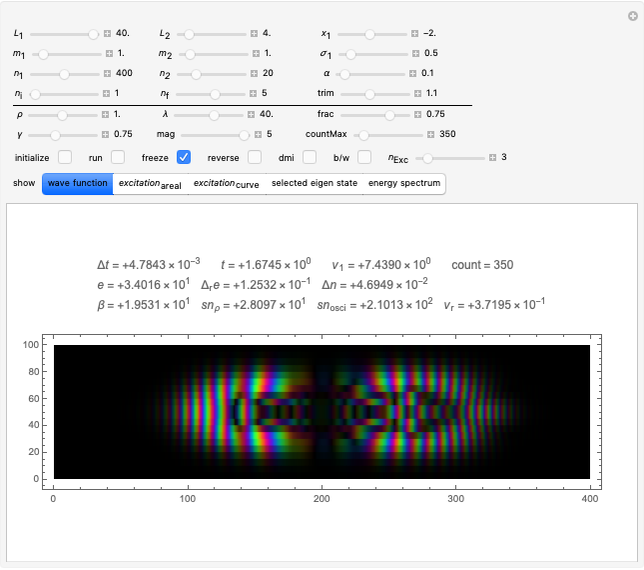
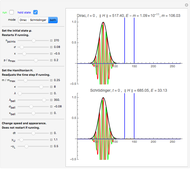
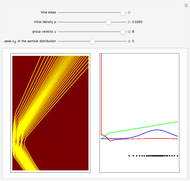
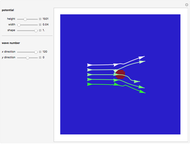
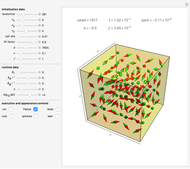
Snapshot 3: Again 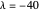 , but in a representation mode that is explained in the annotation to the selected show box. Here the black-and-white mode is used, since it improves the visibility of the dark stripe patterns, which are reminiscent of photographs of stellar spectra.
, but in a representation mode that is explained in the annotation to the selected show box. Here the black-and-white mode is used, since it improves the visibility of the dark stripe patterns, which are reminiscent of photographs of stellar spectra.
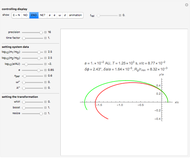
The motivation for considering the crossway system is more fully described in [1, Section 5]. It should be noted that the default integrator of this Demonstration is different from the one employed in [1]. It is the method DALF of [2]. The numbers in this program may refer to any system of units for length, time and mass, setting 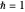 .
.
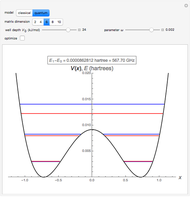
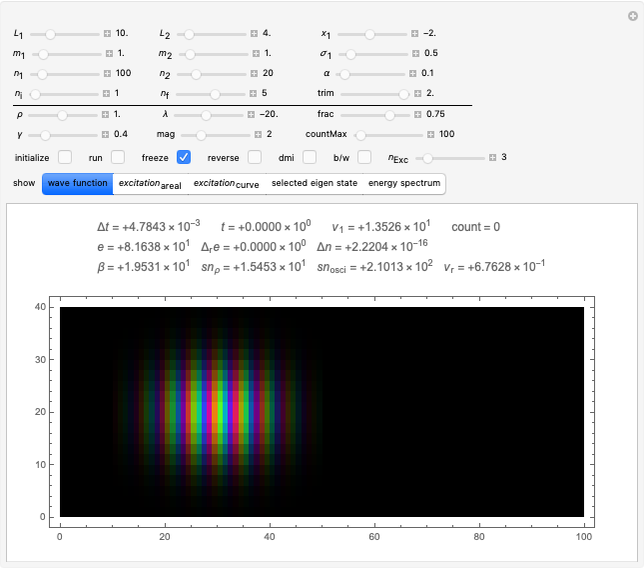
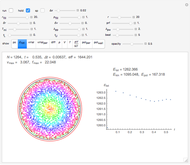
Some remarks concerning usage of the controls: The controls fall into two groups, separated by a horizontal black line. If the Manipulate is evaluated the first time it computes the default initial state and prepares it for executing the time evolution algorithm, without starting it. To start it, one has to check the 'run'-box. To start from a different initial state one may perform any modification to the controls. If the settings are as wanted, one has to check the 'initialize'-box. Again, checking the 'run'-box asks for starting the time evolution. Before it actually starts (there is a counter to show this) it may take a while if the integers 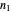 and
and 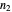 were chosen quite large. While running the program allows to manipulate the controls below the black horizontal line. For inspection of details one may toggle the 'run'-box arbitrarily often. By changing 'countMax' one may continue the run if it arrived to its preset end.
were chosen quite large. While running the program allows to manipulate the controls below the black horizontal line. For inspection of details one may toggle the 'run'-box arbitrarily often. By changing 'countMax' one may continue the run if it arrived to its preset end.
References
[1] U. Mutze. "The Direct Midpoint Method as a Quantum Mechanical Integrator." (Oct 4, 2019) www.ma.utexas.edu/mp_arc/c/06/06-356.pdf.
[2] U. Mutze, "An Asynchronous Leapfrog Method II." www.arxiv.org/abs/1311.6602.
Permanent Citation