The Difference between European Option Prices in the Black-Scholes and NIG Models Computed with the DFT

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
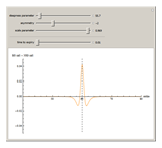
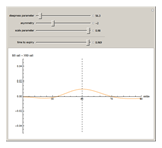
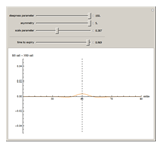
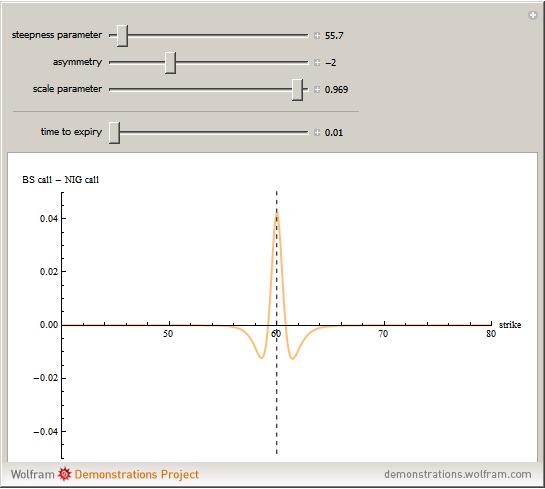
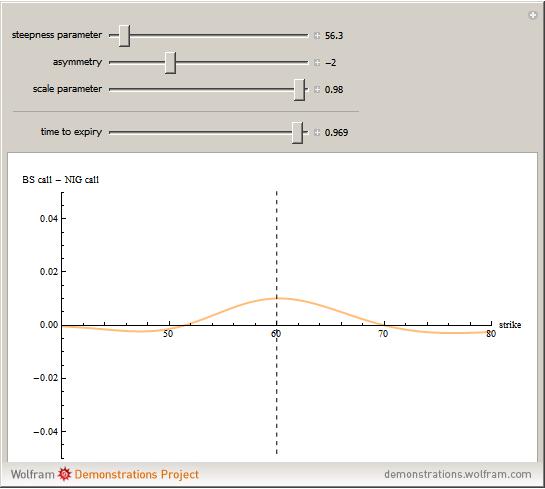
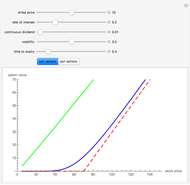
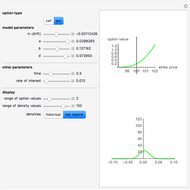
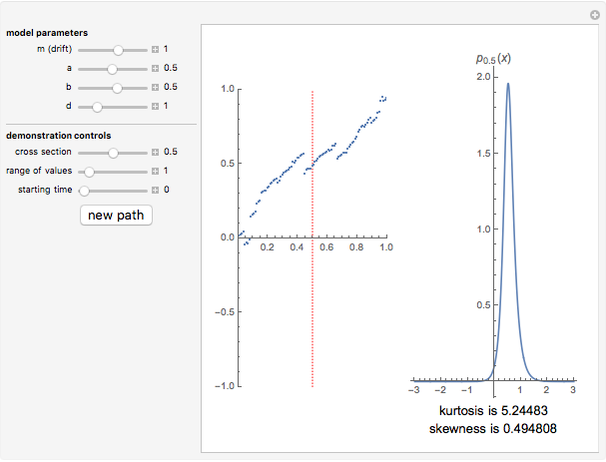
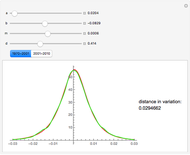
This Demonstration shows the difference between the price of a European call option on stock (no dividend is paid and the interest rate is 0) in the Black–Scholes model and the model (due to Barndorff–Nielson) based on a centered exponential Normal Inverse Gaussian (NIG) Lévy process, as a function of the strike price. There are three model parameters that control the NIG process: steepness, asymmetry, and scale (the fourth parameter, location, is set to 0). The other control parameter is the time to expiry of the option.
[more]
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The NIG process has been shown by several empirical studies to model option prices more accurately than the Black–Scholes model. Unlike the Black–Scholes model, there is no unique non-arbitrage price in the NIG model (and in other incomplete models, e.g. those involving jumps or stochastic volatility), so the price has to be chosen using economic considerations. We use the price given by replacing the real world measure by the equivalent martingale measure defined by means of the Esscher transform (see [2]). The prices for both models are computed for a range of strike prices using the discrete Fourier transform (DFT) following the method described in [1] and generalized in [3]. The method of computing NIG option prices used in this Demonstration is due to Gerber and Shiu [1]. A detailed study of option pricing with Lévy processes, of which the NIG process is an example, can be found in [2].
[1] P. Carr and D. B. Madan, "Option Valuation Using the Fast Fourier Transform," The Journal of Computational Finance, 2(4), 1999.
[2] H. U. Gerber and E. S. W. Shiu, "Option Pricing by Esscher Transforms," Transactions of the Society of Actuaries, 46, 1999 pp. 99–191.
[3] S. Raible, Lévy Processes in Finance: Theory, Numerics, and Empirical Facts, PhD thesis, University of Freiburg, 2000.