A Minimal Circumcircle Measure of District Compactness

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The United States Constitution prohibits states from "denying any person within its jurisdiction the equal protection of the laws". Various decisions of the United States Supreme Court have interpreted this provision to constrain the otherwise existing freedom of the states to draw political districts in ways that disadvantage racial, ethnic or other protected groups. Districts that are not "compact" are subject to heightened scrutiny for evidence of racial or other prohibited biases.
[more]
Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
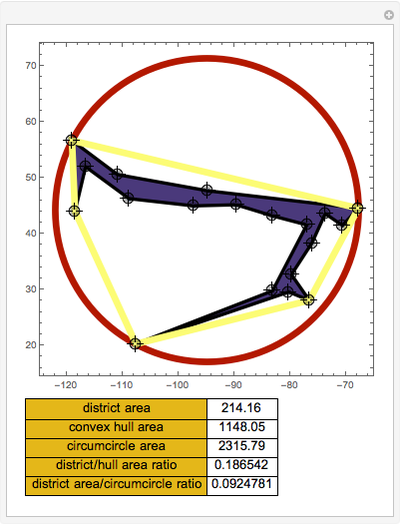
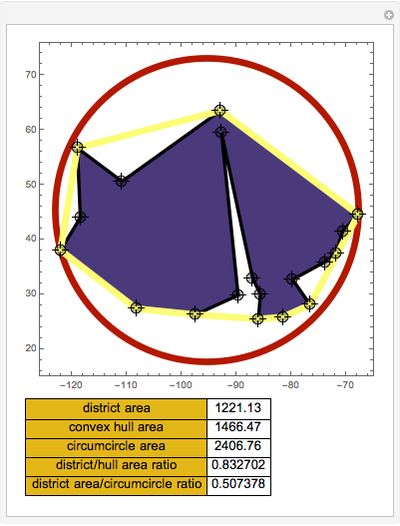
The formulas provided in this Demonstration will give an erroneous answer for polygons that self-intersect.
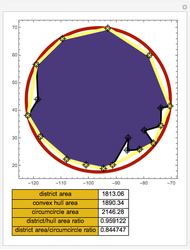
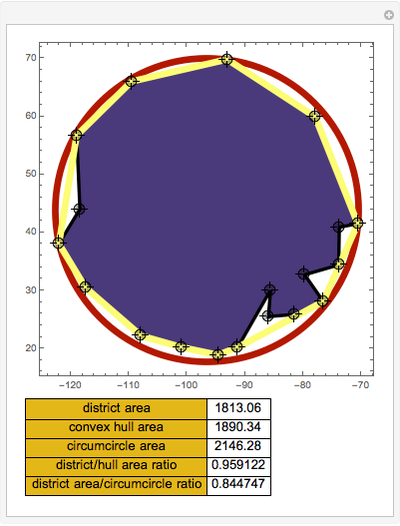
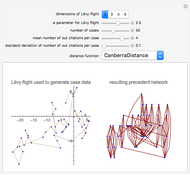
Snapshot 1: a very compact district
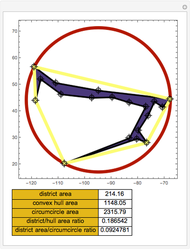
Snapshot 2: a very noncompact district
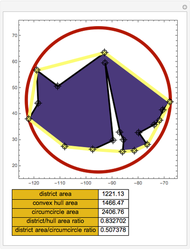
Snapshot 3: a moderately compact district
Snapshot 4: a convex quadrilateral district with moderate compactness
C. Chambers and A. Miller, "Measure of Bizarreness".
E. C. Reock, "A Note: Measuring Compactness as a Matter of Legislative Apportionment," Midwest Journal of Political Science, 5(1), 1961 pp. 70–74.
Permanent Citation
"A Minimal Circumcircle Measure of District Compactness"
http://demonstrations.wolfram.com/AMinimalCircumcircleMeasureOfDistrictCompactness/
Wolfram Demonstrations Project
Published: March 7 2011