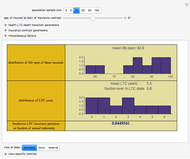
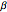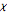A Parameterized Multistate Life Table

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
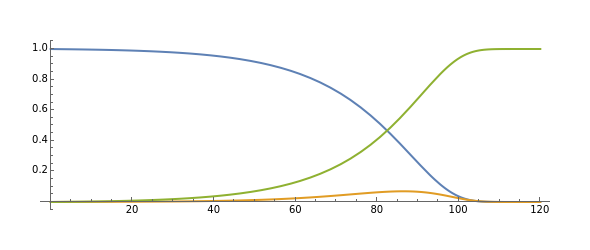
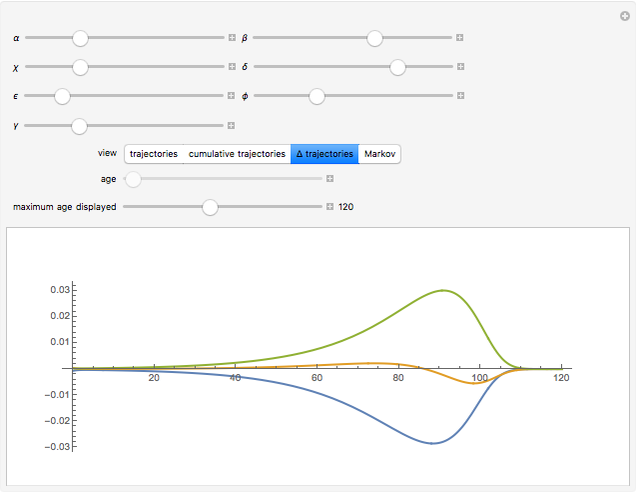
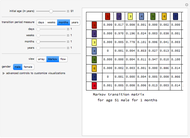
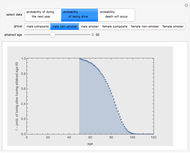
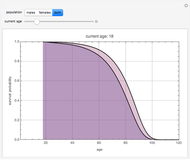
Actuarial computations involving life insurance generally require computing probabilistic trajectories involving only two possible states: at any moment in time the person is either alive or dead. Actuarial computations involving disability insurance, long-term care insurance, or other long-term insurance based on health require more complex modeling, however, in which the probabilistic trajectories involve more than two states. This Demonstration illustrates a three-state model in which the person is either healthy, ill, or dead.
[more]
Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
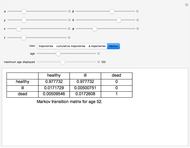
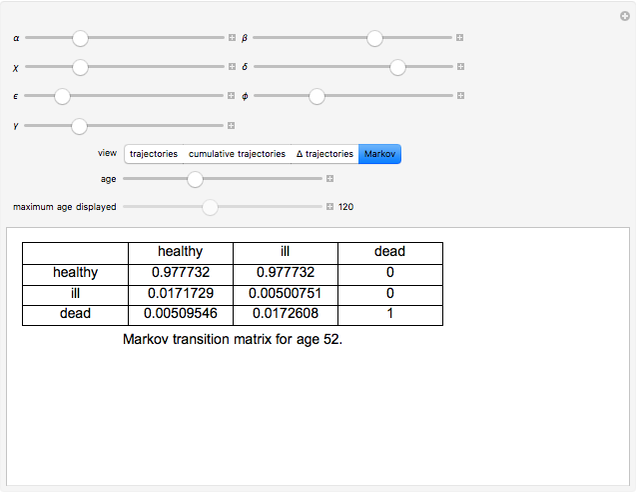
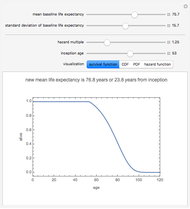
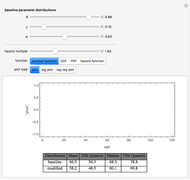
The Demonstration assumes that transitions between the healthy and ill states, the healthy and dead states, and the ill and dead states are all determined by modified Gompertz models. A Gompertz model is one in which the fraction of people changing their status (the logarithmic derivative of status) is a weighted exponential function of time (
 ), where
), where  is the weighting parameter and
is the weighting parameter and  determines the pace of exponential change. Although widely used in actuarial science and generally providing a plausible parameterized description of human mortality, the Gompertz model cannot be correct at high age values. This theoretical problem exists because when
determines the pace of exponential change. Although widely used in actuarial science and generally providing a plausible parameterized description of human mortality, the Gompertz model cannot be correct at high age values. This theoretical problem exists because when  exceeds a critical value (
exceeds a critical value ( ), the function value—the fraction of people changing their status—is greater than one. To prevent this impossibility from occurring as the user changes the parameters, this Demonstration slightly modifies the Gompertz formula. The logarithmic derivative is set equal to an age-based weighted average of the Gompertz function and a constant value. The constant value is set to the value the Gompertz function attains when it is 99% of the critical value. The weighting is the value for a given age of a cumulative logistic distribution centered at 98% of the critical value and with a standard deviation equal to 6.3% of that critical value.
), the function value—the fraction of people changing their status—is greater than one. To prevent this impossibility from occurring as the user changes the parameters, this Demonstration slightly modifies the Gompertz formula. The logarithmic derivative is set equal to an age-based weighted average of the Gompertz function and a constant value. The constant value is set to the value the Gompertz function attains when it is 99% of the critical value. The weighting is the value for a given age of a cumulative logistic distribution centered at 98% of the critical value and with a standard deviation equal to 6.3% of that critical value.
The default values for the Gompertz mortality parameters are the best fit (using Mathematica's built-in function NonlinearModelFit) for data from the 2001 CSO Mortality Tables.
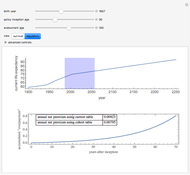
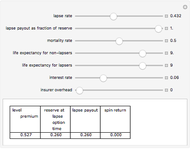
The net premium to break even on a policy that pays in the event of illness and that does not require payment of a premium in the event the person is ill should equilibrate (a) the present value of the probability-weighted state of being ill multiplied by the payment in the event the person is ill; and (b) the present value of premiums multiplied by the probability that the person is healthy. Computation of actuarially fair premiums for "real" illness-based insurance policies is considerably more complicated since such policies generally have deductibles based on the number of days of prior illness and often have limits based on the total number of days of illness.
Permanent Citation