Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Baseball without Swings

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

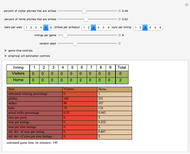
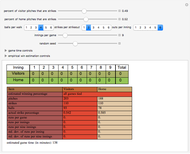
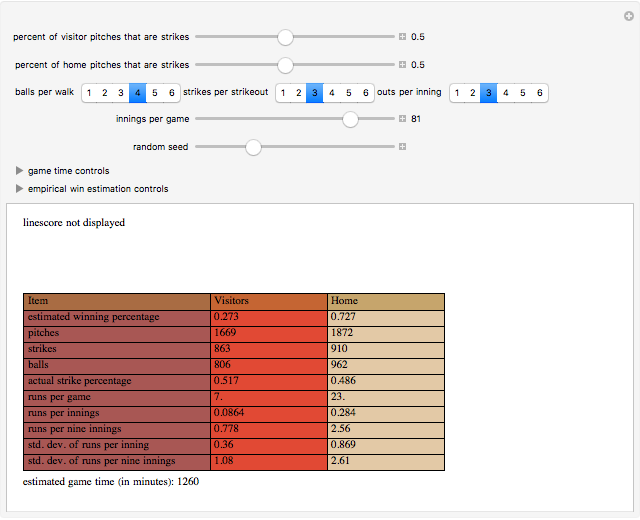
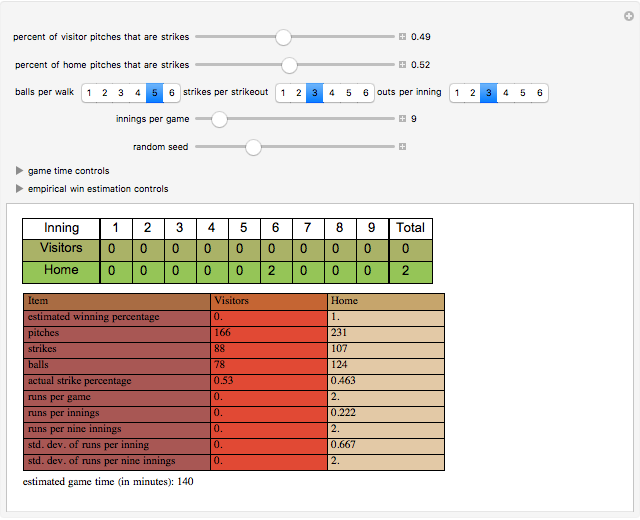
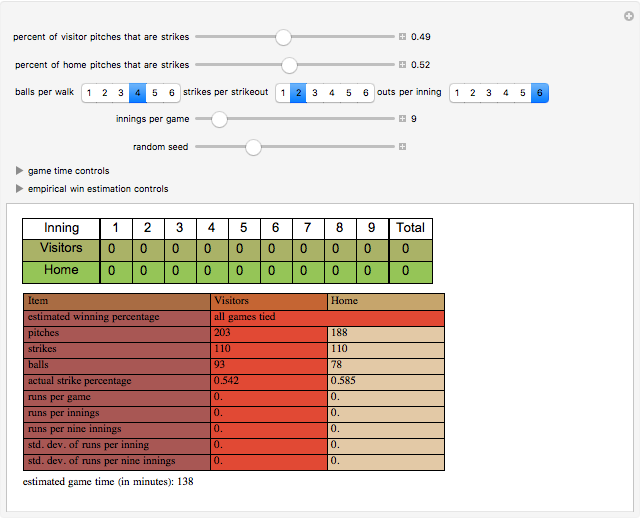
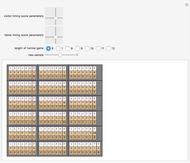
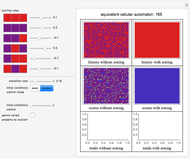
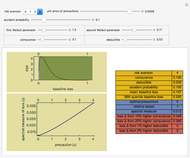
Consider a game modeled after American baseball that involves a "state" that will be altered in a complex way by a sequence of "pitches" that are randomly either a "strike" or a "ball" according to a user-specified ratio. The "state" of the game is an inning integer, an out integer, a run integer, a "line score" substate, a count substate, or a three-element base occupation substate. At the start of the game, the state is {1,0,0,{},{0,0},{False,False,False}}.

[more]

After each pitch, one examines and modifies the state of the game. In Stage 1 of this examination, when a strike is encountered, the second element of the count substate is incremented. When a ball is encountered, the first element of the count substate is incremented. The state is then examined. If the second element of the count is equal to a user-specified value (traditionally 3), the out component of the state is incremented and the count substate is reset to {0,0}. If the first element of the count is equal to a user-specified value (traditionally 4), the count substate is reset to {0,0} and the base occupation substate is examined and potentially modified. If the base occupation substate is {True,True,True}, then the run component of the state is incremented; otherwise, the base occupation substate is rotated to the right and the first element replaced by True.

In Stage 2 of this examination, one examines the out component of the state. If it is equal to a user-specified value, one increments the inning, appends the current run state to the line score substate, resets the runs component to 0, and resets the out component to 0.

One continues this process until the inning component of the state is greater than a user-specified value.

This Demonstration outputs numerous statistics relating to the game created by this process. It outputs a "line score", a grid showing 11 elements of the simulated game, including the estimated "winning percentages" for each team, and an estimated game time. Exploring the controls shows that small changes in the percentage of strikes thrown or in the rules governing the progress of the game can have a dramatic effect on the outcome.

[less]

Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This Demonstration is inspired by watching numerous Little League games and wondering how the team at bat would do if the batters were instructed never to swing at the ball.

There are a number of simplifications made in this simulation, including (1) the absence of batters gaining first base through being hit by a pitch and (2) the absence of stolen bases.

In the major leagues in the United States, approximately 62% of pitches would be strikes if not swung at.

The estimated winning percentage is computed through a bootstrap method in which two arrays (of user-determined dimensions) of random choices are drawn from the line score of the game. One array is for the visiting team and one array is for the home team. Each row of the array is then tallied to determine a final score for each team. The results are then compared game by game to calculate a winning percentage. Ties are discarded. To increase the accuracy of this method, increase the number of innings per game.

The estimated game time is computed as the sum for each team of the number of pitches multiplied by the time between pitches plus the inning change time multiplied by one minus the number of (half) innings.

This Demonstration could be used to optimize rules for baseball that varied depending on the expected skill levels of pitchers in throwing strikes. One could, for example, alter the number of balls per walk, strikes per game, or outs per inning that, for a given expected level of success of pitchers in throwing strikes, would result in traditional scores while permitting the game to move along swiftly.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send