Bohm Trajectories for Quantum Airy Waves in a Time-Dependent Linear Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
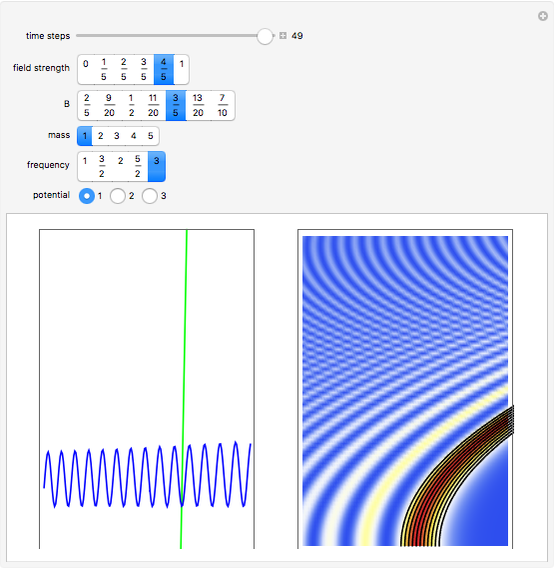
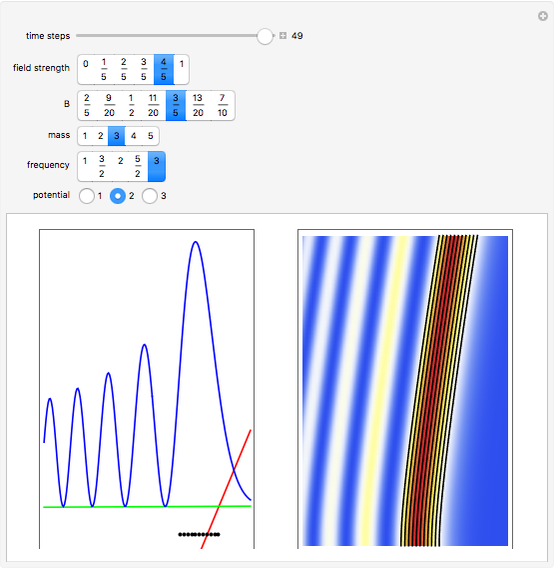
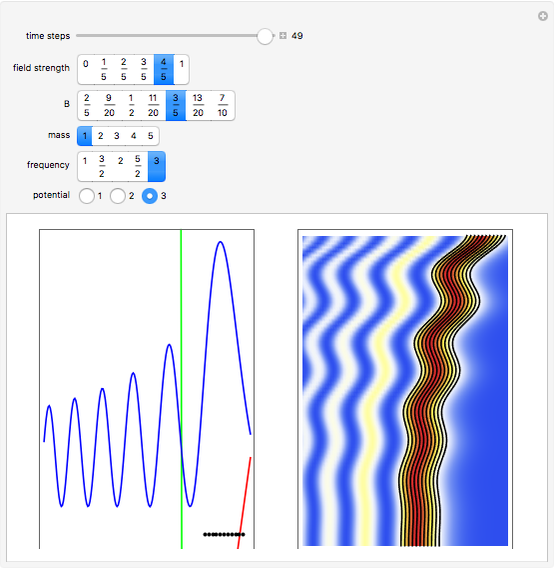
This Demonstration represents the motion of Airy waves according to the causal interpretation of David Bohm and Louis de Broglie. The trajectories are streamlines in the Madelung fluid, regarded as paths of quantum particles, which are not directly measurable. Airy wave packets  take their name from the "Airy integral", introduced by Sir George Biddell Airy in the 1830s to explain optical caustics. Within the context of quantum physics, as described by the Schrödinger equation, Airy waves were initially introduced by Michael Berry and Nandor Balazs. An Airy wave packet does not spread out as it propagates, but it accelerates in free space. This is not a contradiction to Ehrenfest's theorem, because the wave function is not square integrable and hence does not satisfy the initial condition in the proof of the theorem. Therefore, it does not really describe a particle and has no classical counterpart. Nonspreading Airy packets even exist in a time-dependent uniform potential. If the field strength is zero (
take their name from the "Airy integral", introduced by Sir George Biddell Airy in the 1830s to explain optical caustics. Within the context of quantum physics, as described by the Schrödinger equation, Airy waves were initially introduced by Michael Berry and Nandor Balazs. An Airy wave packet does not spread out as it propagates, but it accelerates in free space. This is not a contradiction to Ehrenfest's theorem, because the wave function is not square integrable and hence does not satisfy the initial condition in the proof of the theorem. Therefore, it does not really describe a particle and has no classical counterpart. Nonspreading Airy packets even exist in a time-dependent uniform potential. If the field strength is zero ( ) the Airy wave density propagates freely in configuration space.
) the Airy wave density propagates freely in configuration space.  is an arbitrary constant and the frequency
is an arbitrary constant and the frequency  only occurs in the potential
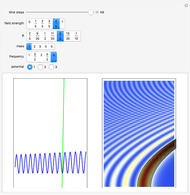
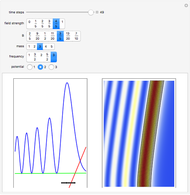
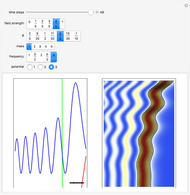
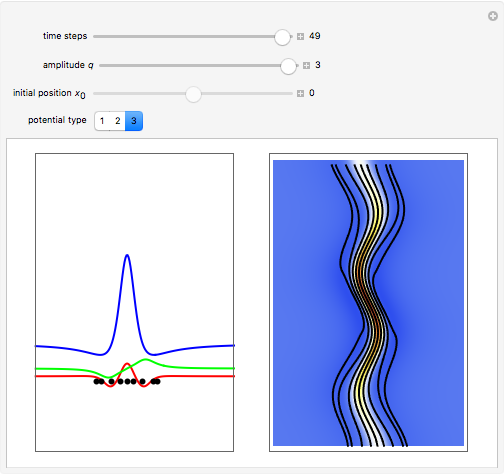
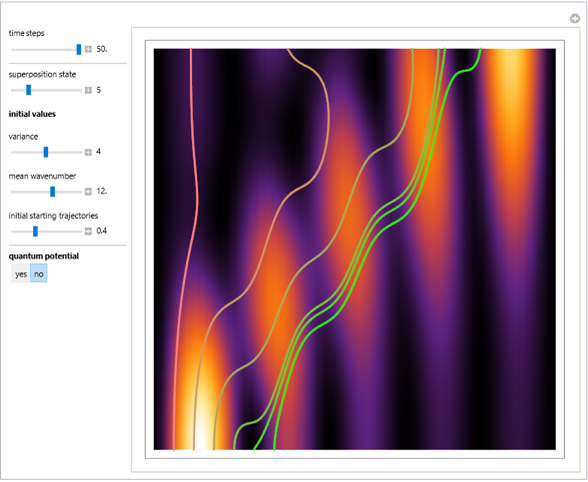
only occurs in the potential  . The quantum motion depends also on the mass. The Airy wave is one of the few examples in which an analytic equation for the quantum motion is obtained. On the left side, you can see the position of the particles, the squared wave function (blue), the quantum potential (red), and the time-dependent uniform potential (green). On the right side, the graphic shows the squared wave function and the trajectories.
. The quantum motion depends also on the mass. The Airy wave is one of the few examples in which an analytic equation for the quantum motion is obtained. On the left side, you can see the position of the particles, the squared wave function (blue), the quantum potential (red), and the time-dependent uniform potential (green). On the right side, the graphic shows the squared wave function and the trajectories.
Contributed by: Klaus von Bloh (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Ehrenfest's theorem asserts that the quantum-mechanical motion of a particle, as represented by the expectation value, should agree with classical mechanics in the correspondence limit. At time  the Airy packet evolves into
the Airy packet evolves into  .
.
Solving 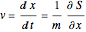 , where
, where 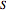 is the real-valued phase function of the wave function in the eikonal form
is the real-valued phase function of the wave function in the eikonal form 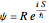 (here
(here 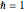 ), yields for the trajectory in
), yields for the trajectory in  ,
, -space:
-space:  .
.
References:
P. Holland, The Quantum Theory of Motion, Cambridge: Cambridge University Press, 1993.
E. Madelung, "Quantentheorie in Hydrodynamischer Form," Z. Phys., 40, 1927 pp. 322–326.
M. V. Berrry and N. L. Balazs, "Nonspreading Wave Packets," Am. J. Phys., 47, 1979 pp. 264–267.
Permanent Citation