Mixing of Quantum Particles Influenced by Nodal Points in the Causal Interpretation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
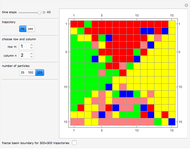
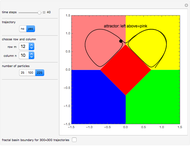
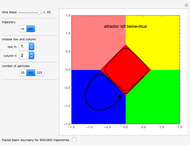
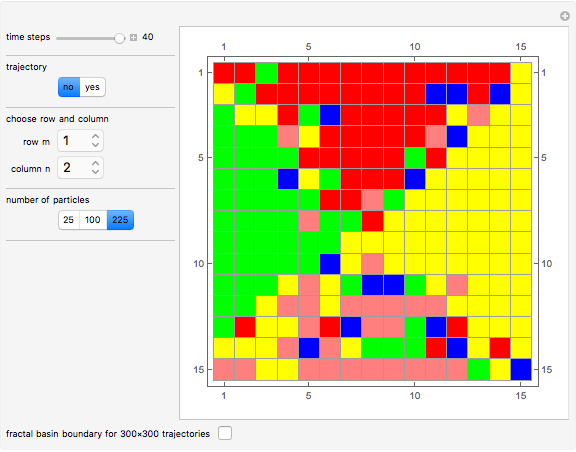
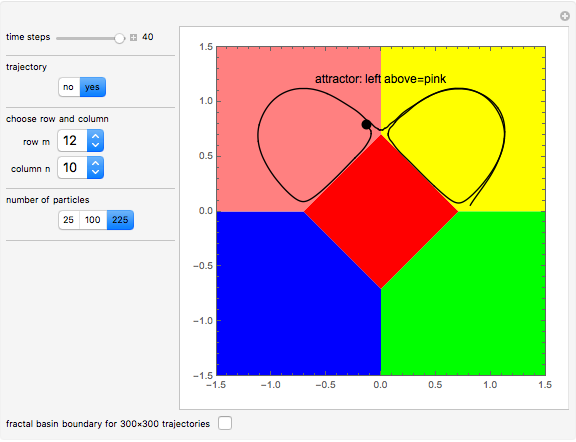
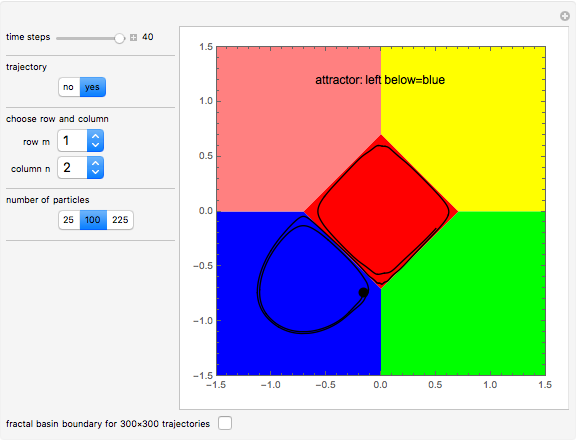
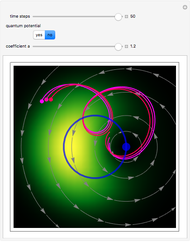
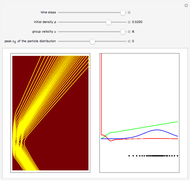
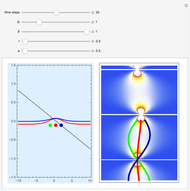
According to the causal interpretation of quantum theory, particles move in a deterministic orbit under the influence of the external potential plus a quantum potential generated by the wavefunction. These orbits can be examined with the tools of classical chaos theory. In this Demonstration a fractal basin boundary is found in an unnormalized, isotopic, two-dimensional harmonic oscillator with a constant phase shift, where the trajectories show chaos. Five moving nodal points (shown in gray) act like attractors protected by limit cycles or as a repeller, in which the quantum trajectories avoid approaching nodal points too closely. Further nodal points form saddle points with respect to the velocity, where the trajectories of the quantum particles become unstable and bifurcation of the trajectories occurs [1]. The attractors generate limited zones of configuration space to which the trajectories (originating from typical initial conditions) tend as time increases. The set of the initial conditions that converge to an attractor is called its basin; the boundary with fractal structures is called the fractal basin boundary or basin of attraction [2]. For each such nodal point, its basin of attraction depends on the set of initial conditions leading to longtime behavior of the trajectory that approaches that attractor. These boundary regions of the attracting nodal points have fractal structures. The graphics show the zones of attraction in relation to the starting points of the trajectories at given times and the trajectories in the two-dimensional configuration space. Each color defines an approximate attractor zone, to which the trajectories converge as time increases.
Contributed by: Klaus von Bloh (September 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The wavefunction obeys the Schrödinger equation:
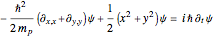 ,
,
with 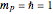 ,
,  , and so on. The unnormalized wavefunction is:
, and so on. The unnormalized wavefunction is:
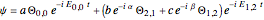 ,
,
with the eigenfunctions 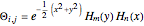 , where
, where 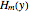 ,
, 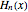 are Hermite polynomials. The parameters
are Hermite polynomials. The parameters  ,
,  ,
,  are arbitrary constants (here:
are arbitrary constants (here: 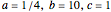 ), and
), and  ,
, 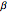 are constant phase shifts (
are constant phase shifts (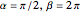 ), and the quantum numbers
), and the quantum numbers 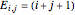 with
with 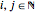 . The velocity field
. The velocity field 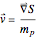 is calculated from the gradient of the phase from the total wavefunction in the eikonal form
is calculated from the gradient of the phase from the total wavefunction in the eikonal form  .
.
Due to limitations of CPU power, AccuracyGoal, PrecisionGoal,and MaxSteps are decreased and the estimation of the nodal points are deactivated. So, be careful: the orbits have only qualitative character because of the inaccuracy of the numerically integrated functions.
References
[1] C. Efthymiopoulos, C. Kalapotharakos, and G. Contopoulos, "Origin of Chaos near Critical Points of the Quantum Flow," Physical Review E, 79, 2009 pp. 036203–1–036203–18. doi:10.1103/PhysRevE.79.036203, arXiv:0903.2655 [quant-ph].
[2] H-O. Peitgen and P. H. Richter, The Beauty of Fractals, Berlin: Springer-Verlag, 1986.
Permanent Citation