Nash Equilibria with Continuous Strategies

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
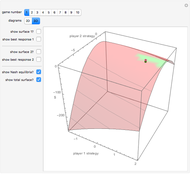
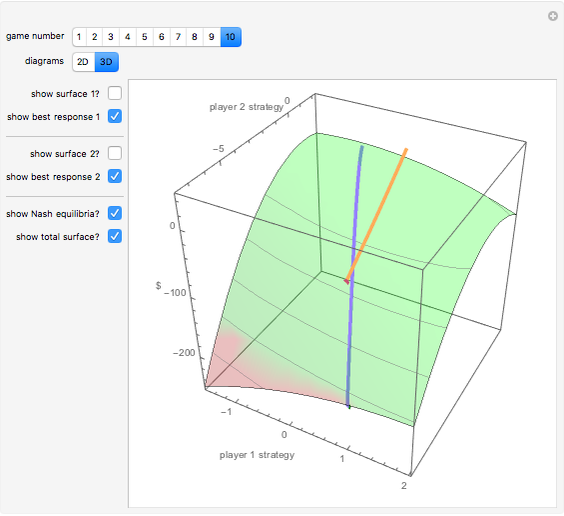
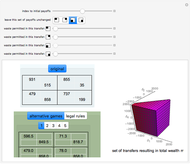
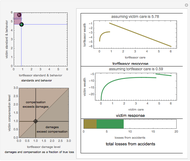
A Nash equilibrium of a game is a strategy combination such that no party can improve its situation by changing its strategy, assuming the complementary strategies of the other players stay the same. The strategies are said to be "mutual best responses." This Demonstration lets you examine 10 continuous strategy games and see the payoff surfaces of each of the players as well as the sum of the payoffs. These surfaces can be visualized in three dimensions or in two dimensions. The Demonstration also calculates "best response" curves for each of the players, shown in orange and blue, respectively, and projects the Nash equilibrium point onto each best response curve. The total payoff surface is colored green for those strategy combinations that would improve total wealth relative to that achieved at the Nash equilibrium. The "green zone" thus represents the strategy combinations that, if wealth were transferrable between the players through enforceable contracts, would be Pareto superior to the Nash equilibrium.
Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
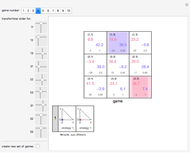
In the two-dimensional graphic, player 1's contours are colored aqua, player 2's contours are colored pink, and the total contours are colored violet.
Snapshot 1: a contour plot of the payoff surfaces and total surface
Snapshot 2: the graphic in which only the total payoffs are showing
Snapshot 3: a scenario in which the loss resulting from playing non-cooperatively can be quite large; the graphic has been rotated and the player payoff surfaces deleted for clarity
Permanent Citation
"Nash Equilibria with Continuous Strategies"
http://demonstrations.wolfram.com/NashEquilibriaWithContinuousStrategies/
Wolfram Demonstrations Project
Published: March 7 2011