Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Estimating Insurance Premiums Using Exceedance Data and the Method of Moments

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Some experts in finance theorize that the "fair" price for a layer of insurance is a linear combination of (1) the expected losses of that layer; and (2) the increment to the insurer's standard deviation of losses in its portfolio caused by assumption of that layer of insurance. This Demonstration explores the implications of this theory by letting you set the cumulative density function for some risk, the layer of losses that will be insured, and the linear combination of expected loss and standard deviation of loss that predict the premium.

[more]

You move locators to set the cumulative density function and use the setter bar at the top to determine the family of distributions for which parameters are to be estimated. The Demonstration responds by determining the parameters of that distribution whose first two moments match the observed values.

A second part of the Demonstration lets you use the computed probability distribution. You move the sliders to establish a layer (or "tranche", as it is often known) for which an insurer has responsibility. An insurer might, for example, have to pay the difference between the insured's loss and 0.6, with that value clipped between zero and 0.5. In the trade, this would be called a "0.5 XS 0.6 policy". The Demonstration uses the computed probability distribution to determine the expected value and standard deviation of the payments an insurer writing such a tranche would face. It then uses a conventional load coefficient and risk load coefficient that you set to determine the premium an insurer writing this layer would likely charge. The increment to the standard deviation of losses in the insurer's portfolio is approximated as a value proportional to the standard deviation of the losses of the specified layer of insurance.

[less]

Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

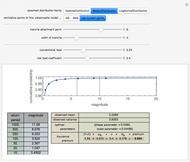
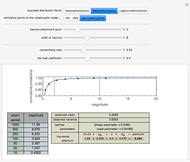
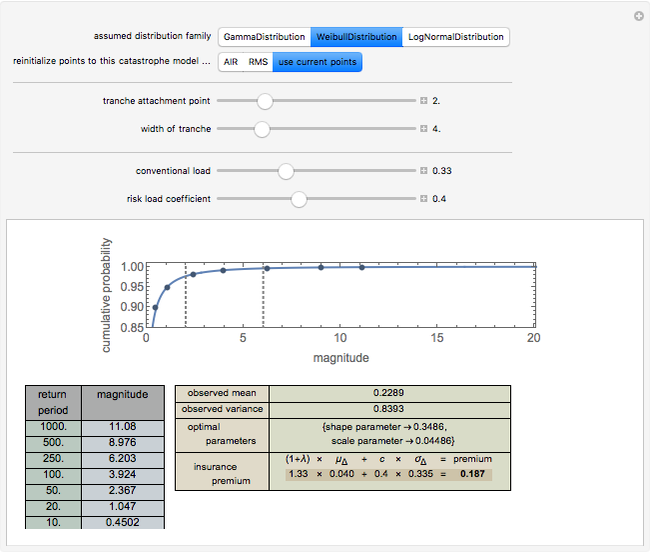
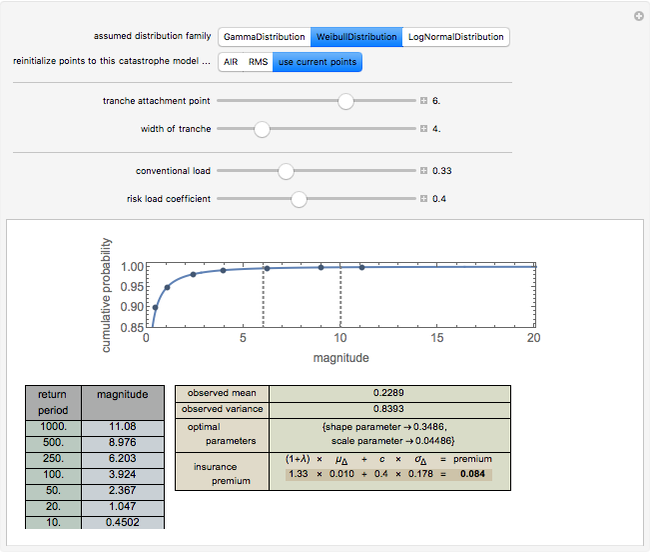
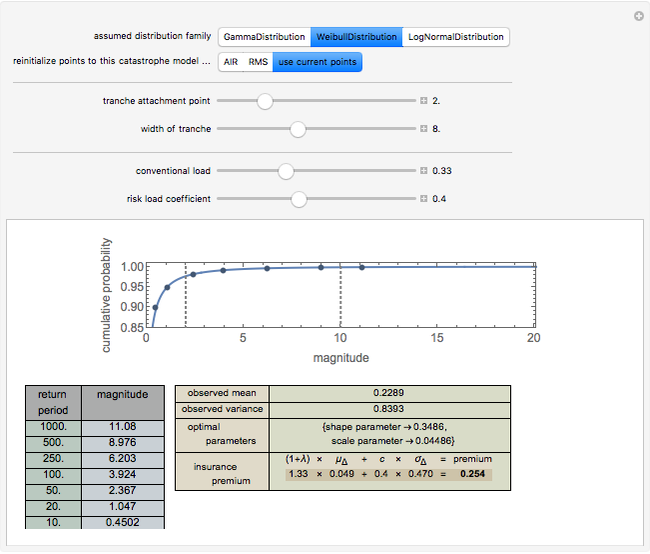
The default data is taken from work submitted by the Texas Windstorm Insurance Association (TWIA) to regulators in 2008 regarding the likely magnitude of insured damages caused by hurricanes striking the Texas coast during the forthcoming 2008-09 hurricane season. The data was originally generated by the catastrophe modeling firms AIR Worldwide Corporation (AIR) and Risk Management Solutions, Inc. (RMS). You can reinitialize the points to correspond with these estimates. All numbers are actually in billions of dollars.

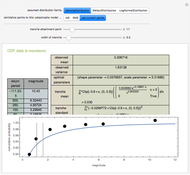
The method of moments has the virtue of being extremely fast; it is not, however, a maximum likelihood estimator.

Snapshot 1: Using the AIR data and a Weibull distribution, conventional load of 0.33, and a risk load of 0.4, the premium for a 4 XS 2 tranche is 0.187.

Snapshot 2: Using the AIR data and a Weibull distribution, conventional load of 0.33, and a risk load of 0.4, the premium for a 4 XS 6 tranche is 0.084.

Snapshot 3: Using the AIR data and a Weibull distribution, conventional load of 0.33, and a risk load of 0.4, the premium for an 8 XS 2 tranche is 0.254.

A comparison of snapshot 3 with snapshots 1 and 2 shows that the linear combination model has the "feature" that the premium for a set of layers is not equal to the sum of the premiums for the layers. This distressing failure of "conservation" may be a result of the use of an approximation in this implementation of the model. The original proponents of the model argue that one should use not the standard deviation of the risk but the increment to the standard deviation of a portfolio of risks caused by the assumption of the particular risk. This Demonstration approximates the correct statistic by in effect taking the standard deviation of the particular risk and then multiplying by a lower coefficient. While this approximation probably works tolerably in many settings, it can lead to problematic consequences.

Snapshot 4: Using the RMS data and a Weibull distribution, conventional load of 0.33, and a risk load of 0.4, the premium for an 8 XS 2 tranche is 0.203. The selection of a dataset can thus have a significant effect on estimated premiums.

Snapshot 5: Using the RMS data and a gamma distribution, conventional load of 0.33 and a risk load of 0.4, the premium for an 8 XS 2 tranche is 0.108. The selection of a distribution family can thus have a significant effect on estimated premiums.

Snapshot 6: A non-monotonic cumulative distribution function leads to various error messages.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send