Semiclassical Approximation for Quantum Harmonic Oscillator Wavefunctions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
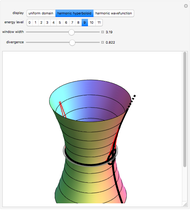
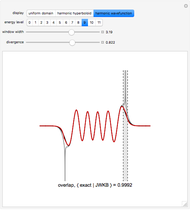
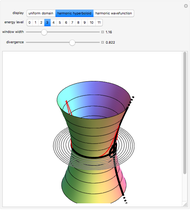
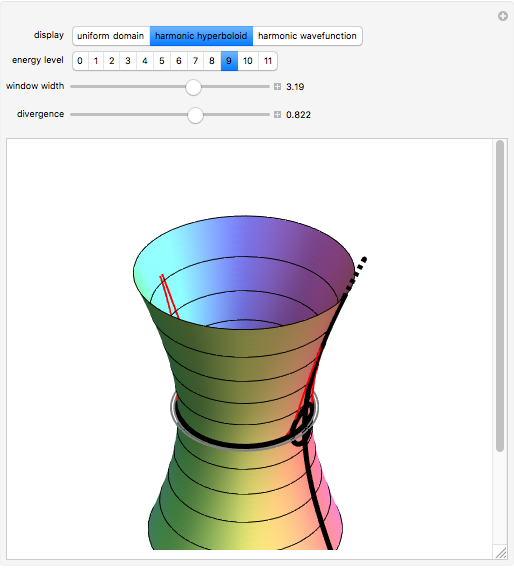
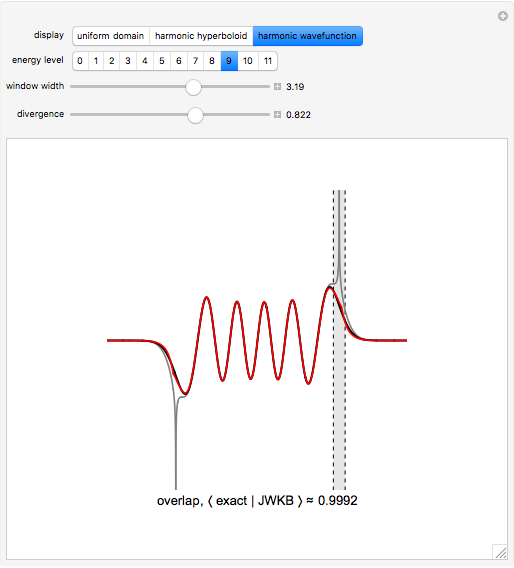
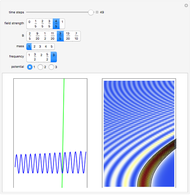
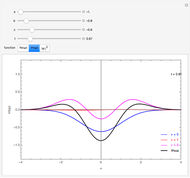
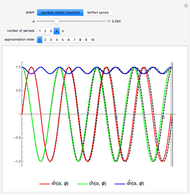
In semiclassical mechanics, wavefunction shapes are not entirely easy to determine; however, the Jeffreys–Wentzel–Kramers–Brillouin (JWKB) approximation gives an explicit and intuitive prescription [1, 2]. Testing on the quantum harmonic oscillator shows that a typical JWKB approximation accurately recreates the exact solution, except in the immediate vicinity of the turning points. To attain 99.8% or 99.9% agreement on the entire domain, we advance a two-parameter ansatz that relaxes the integration contour along the surface of a Riemannian harmonic hyperboloid (see Details).
Contributed by: Brad Klee (December 2016)
Open content licensed under CC BY-NC-SA
Details
The JWKB approximation follows from the assumption of an exponential form for the configuration-space wavefunction  [1, 2]. To first order in a small parameter
[1, 2]. To first order in a small parameter  , the approximation works out as an integral over recognizable classical variables,
, the approximation works out as an integral over recognizable classical variables,
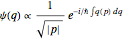 ,
,
with domain 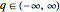 . Harmonic oscillation involves a purely quadratic Hamiltonian constraint,
. Harmonic oscillation involves a purely quadratic Hamiltonian constraint, 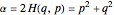 . The energy variable
. The energy variable  is quantized according to a stationary phase condition,
is quantized according to a stationary phase condition,
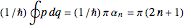 ,
,
where offset  follows from the accumulation of phase shifts
follows from the accumulation of phase shifts  at both turning points [1]. A wavefunction
at both turning points [1]. A wavefunction  is associated with each quantized energy
is associated with each quantized energy 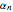 . Complete specification of each
. Complete specification of each 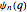 requires superposition of left and right moving sinusoidal waves in the classically allowed region, where
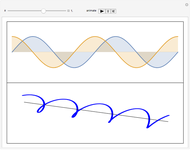
requires superposition of left and right moving sinusoidal waves in the classically allowed region, where  , and attaches exponentially decaying evanescent solutions in the classically forbidden regions, where
, and attaches exponentially decaying evanescent solutions in the classically forbidden regions, where 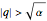 . To construct such a solution in practice, we need to develop more complex geometry.
. To construct such a solution in practice, we need to develop more complex geometry.
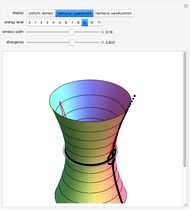
Identifying complex coordinates,  , allows for construction in the four-dimensional space spanned by
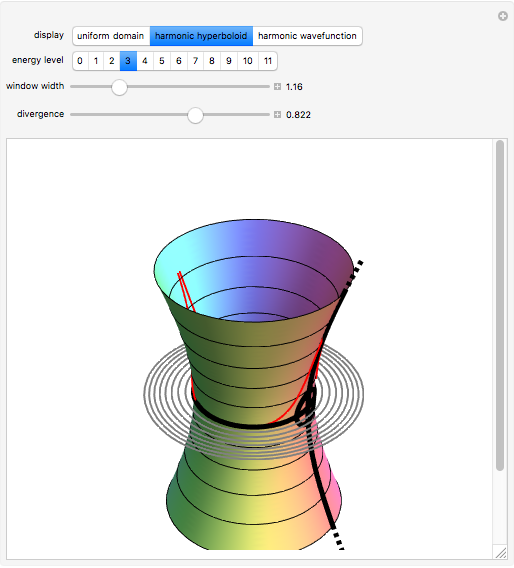
, allows for construction in the four-dimensional space spanned by 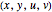 . Here the quadratic Hamiltonian determines a two-dimensional Riemannian surface, the harmonic hyperboloid,
. Here the quadratic Hamiltonian determines a two-dimensional Riemannian surface, the harmonic hyperboloid,
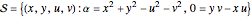 ,
,
with a time-parametrization given as
 .
.
Complex time, 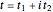 , is said to provide a uniform domain for the surface
, is said to provide a uniform domain for the surface 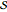 . Trigonometric functions along real-valued coordinate
. Trigonometric functions along real-valued coordinate 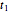 repeat after an interval of
repeat after an interval of 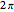 , while the hyperbolic functions along real-valued coordinate
, while the hyperbolic functions along real-valued coordinate 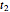 never repeat. Single periodicity clearly identifies the genus
never repeat. Single periodicity clearly identifies the genus  . For an alternative proof, we introduce a new coordinate
. For an alternative proof, we introduce a new coordinate 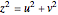 and write
and write
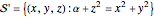 ,
,
which only loses a phase degree of freedom relative to four-dimensional surface 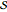 . Level sets along the
. Level sets along the  axis are circles of increasing radius, and these are in bijection with the level sets of a projective sphere. For describing surfaces
axis are circles of increasing radius, and these are in bijection with the level sets of a projective sphere. For describing surfaces 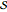 and
and 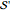 , the adjective "Kleinian" may be more apt, as Riemann reportedly did not think in terms of uniform domains [3].
, the adjective "Kleinian" may be more apt, as Riemann reportedly did not think in terms of uniform domains [3].
Back to quantum mechanics, the JWKB approximation imposes a restriction 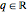 or
or 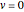 , which limits a single integration contour between
, which limits a single integration contour between 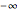 and
and  ,
,
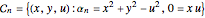 .
.
Unfortunately, integration along this contour goes through a branch point where 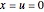 , and the approximation necessarily diverges as
, and the approximation necessarily diverges as 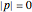 . Instead we avoid the turning point with an ansatz,
. Instead we avoid the turning point with an ansatz,
 ,
,
which maps range  onto a finite domain
onto a finite domain 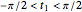 . Changing parameters, we may then calculate the wavefunction in parametric form,
. Changing parameters, we may then calculate the wavefunction in parametric form,
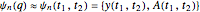 ,
,
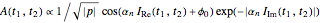 ,
,
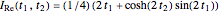 ,
,
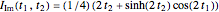 ,
,
with dependence of 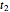 upon
upon 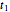 suppressed, and
suppressed, and 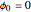 or
or 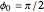 for even or odd parity. In making this approximation, we simply ignore small, nonzero values of the imaginary part
for even or odd parity. In making this approximation, we simply ignore small, nonzero values of the imaginary part 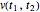 and assume that
and assume that 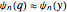 .
.
The ansatz parameters 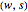 explore a space of trial wavefunctions, which includes the JWKB solution in a limit where
explore a space of trial wavefunctions, which includes the JWKB solution in a limit where 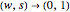 . Decreasing
. Decreasing  from
from 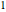 toward
toward  relaxes the wavefunction and smooths out the divergences. Meanwhile parameter
relaxes the wavefunction and smooths out the divergences. Meanwhile parameter 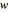 limits deviation from JWKB to a window of finite width. In this Demonstration, optimal values for parameters
limits deviation from JWKB to a window of finite width. In this Demonstration, optimal values for parameters 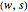 can be found by quick overlap comparison with exact wavefunctions. Although nonstandard, this approach yields good-enough agreement to be considered effective in its own right.
can be found by quick overlap comparison with exact wavefunctions. Although nonstandard, this approach yields good-enough agreement to be considered effective in its own right.
References
[1] E. J. Heller, The Semiclassical Way to Dynamics and Spectroscopy, Princeton, NJ: Princeton University Press, 2018.
[2] M. S. Child, Semiclassical Mechanics with Molecular Applications, New York: Oxford University Press, 1991.
[3] J. J. Gray, Linear Differential Equations and Group Theory from Riemann to Poincaré, 2nd ed., Boston: Birkhäuser, 2008.
Snapshots
Permanent Citation