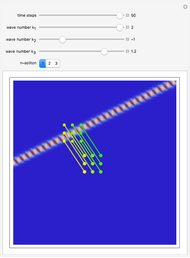
Soliton Trajectories According to Bohmian Quantum Mechanics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
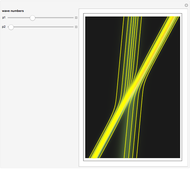
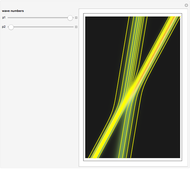
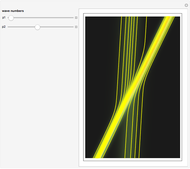
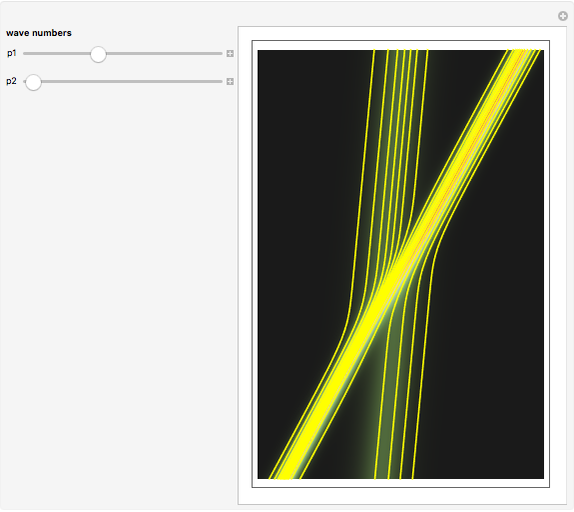
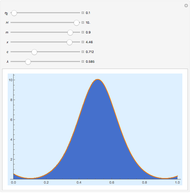
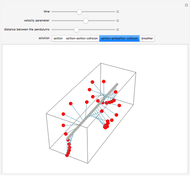
This Demonstration presents the motion of idealized particles inside a two-soliton using the Korteweg–de Vries equation (KdV): 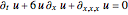 in
in 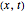 space. The interaction of a two-soliton depends on the wave numbers p1 and p2 that are related via the dispersion relation to the speed of the each wave. In this case
space. The interaction of a two-soliton depends on the wave numbers p1 and p2 that are related via the dispersion relation to the speed of the each wave. In this case 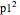 and
and 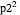 are the velocities of the two solitary waves. The motion of the particles is governed by the current flow, which is derived from the continuity equation
are the velocities of the two solitary waves. The motion of the particles is governed by the current flow, which is derived from the continuity equation 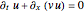 directly. The guidance equations are based only on the velocity, which is
directly. The guidance equations are based only on the velocity, which is 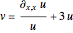 . With
. With 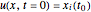 we get the starting points of possible trajectories inside the wave that are distributed according to the density of the wave and lead to single trajectories:
we get the starting points of possible trajectories inside the wave that are distributed according to the density of the wave and lead to single trajectories: 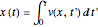 . For the calculation an initial Gaussian distribution is chosen. The system is time reversible:
. For the calculation an initial Gaussian distribution is chosen. The system is time reversible: 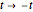 .The concept is based on the causal interpretation of quantum mechanics developed by David Bohm.
.The concept is based on the causal interpretation of quantum mechanics developed by David Bohm.
Contributed by: Klaus von Bloh (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Soliton Trajectories According to Bohmian Quantum Mechanics"
http://demonstrations.wolfram.com/SolitonTrajectoriesAccordingToBohmianQuantumMechanics/
Wolfram Demonstrations Project
Published: March 7 2011