Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Causal Interpretation of Exciting an Atom by Absorption of Intense Light

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

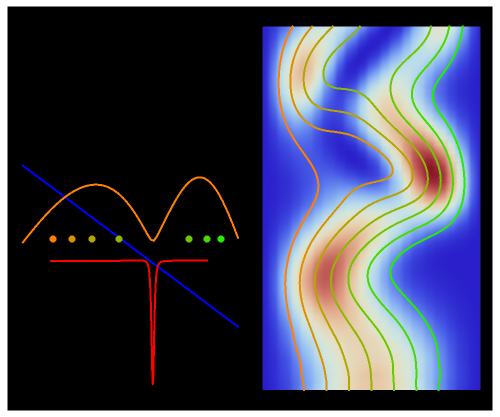
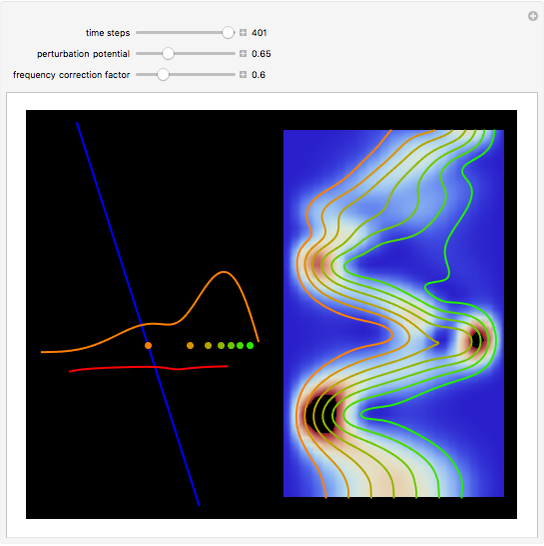
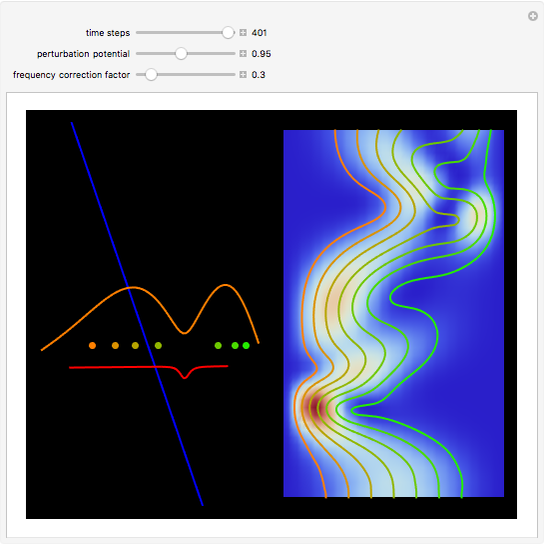
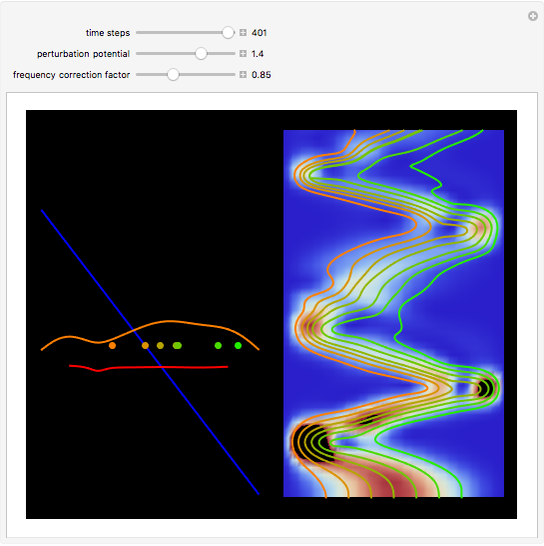
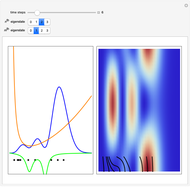
The process of exciting an atom involves adding energy. In the photoelectric effect, electrons are emitted when they absorb energy from incident radiation with a certain minimum frequency . This Demonstration shows only the energy transition of a perturbed atom. An atom is described by a wave in a box with infinitely high walls. For this particular case, the atom is perturbed by a strong periodic external potential, which could be interpreted as a weak or intense electric field with an electric field strength 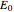that oscillates with some angular frequency . The absorption (or emission) of energy could be described by the transition frequency of the adjacent quantum energylevel 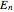, which is 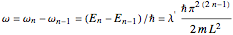(here, with frequency correction factor 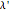, mass , , box length , and energy eigenvalue ). 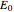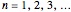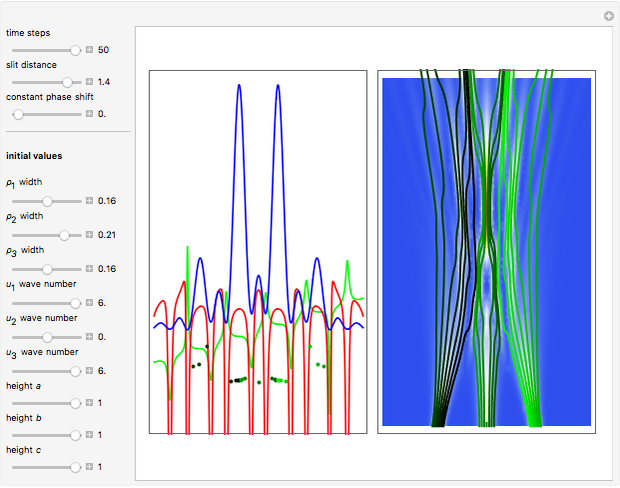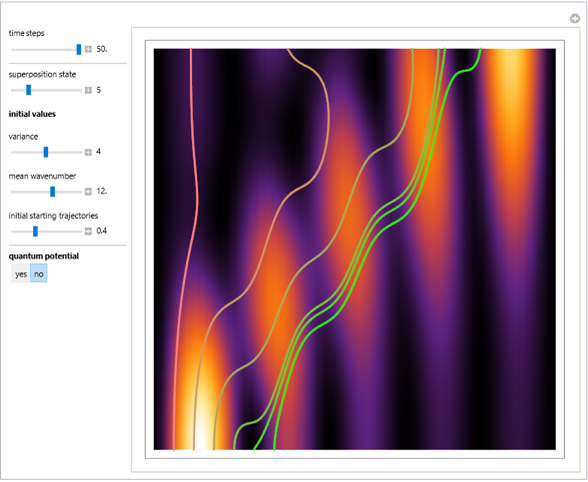Only for definite values of the frequency (by a given strength of the perturbation), depending on the energy eigenvalues , can the atom undergo a transition from the first to the second excited state. If the perturbation term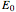 becomes large, the quantum state evolves into a superposition of states with different energy. These mixed states lead to ergodic motion of the quantum particle. The excited atom can be measured by removing the confining well; then the particle moves away faster because of the excited state. The simplicity of the model neglects quantization of the transition-inducing field and other radiation effects.

[more]

In the causal interpretation, the particle position is well-defined and the situation is described by a wavefunction (and a quantum potential) that evolves continuously according to the Schrödinger equation and by the particle positions that change continuously according to the guiding equation.

The trajectories are given as curves along the velocity field given by the quantum current. While the particle positions are measurable in the usual way (the statistics are given by ), a normal position measurement always disturbs the trajectory. Therefore the undisturbed trajectories cannot be measured in the usual way by performing several position measurements in short time intervals. In the causal interpretation there is no evidence of quantum jumps.

The trajectories are positioned in space. The initial positions of the particles are linearly distributed around the peak inside the wave. The graphic on the right shows the squared wavefunction, the potential, and the possible trajectories. The graphic on the left shows the particles' positions, the squared wavefunction (orange), the quantum potential (red), and the potential (blue). The potentials are approximately scaled to fit.

[less]

Contributed by: Klaus von Bloh (April 2013)
Suggested by: Chris Dewdney
Based on a program by: Enrique Zeleny and Paul Nylander
Open content licensed under CC BY-NC-SA

Snapshots

Details

The numerical methods to calculate the velocity and the quantum potential from a discrete function are, in general, not very stable, but the applied interpolation functions lead to an accurate approximation of the physical event.

For speed, contrary to custom the time steps are increased and the mesh points are decreased, so that the final results have only qualitative character in some cases. Further investigations are needed to find precise parameters for the transition process (for an example, see the YouTube video by the author [1].

The author would like to thank Sören Petrat and the team at the department of mathematics of the Ludwig-Maximilians-University Munich (workgroup Bohmian Mechanics) for their helpful suggestions.

References

[1] K. von Bloh. Quantum Time-Dependent Perturbation Theory of the Infinite Potential Wall. [Video]. (Apr 23, 2013) www.youtube.com/watch?v=q5eQf-aecfA.

[2] C. Dewdney and M. M. Lam, "What Happens During a Quantum Transition?," Information Dynamics (H. Atmanspacher and H. Scheingraber, eds.), New York: Plenum Press, 1991.

[3] S. Goldstein. "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy. (Mar 29, 2013)plato.stanford.edu/entries/qm-bohm.

[4] Bohmian-Mechanics.net. (Mar 29, 2013) www.bohmian-mechanics.net/index.html.

[5] Wikipedia. "Crank-Nicolson Method." (Mar 29, 2013) en.wikipedia.org/wiki/Crank-Nicolson_method.

[6] A. Goldberg, H. Schey, and J. L. Schwartz, "Computer-Generated Motion Pictures of One-Dimensional Quantum-Mechanical Transmission and Reflection Phenomena," American Journal of Physics, 35(3), 1967 pp. 177-186. doi:10.1119/1.1973991.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send