Triple-Slit Experiment in the Causal Interpretation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
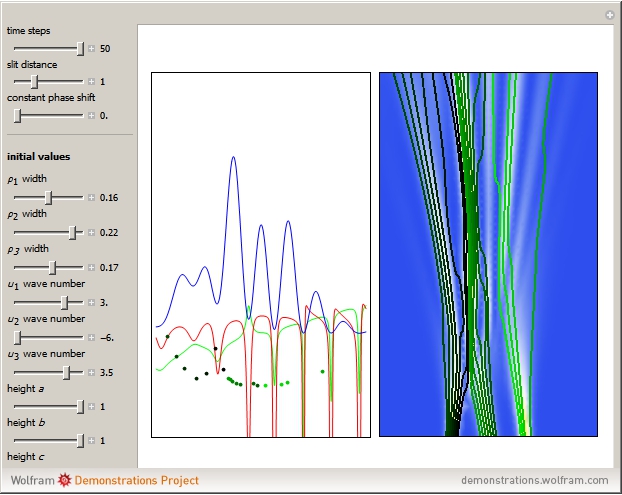
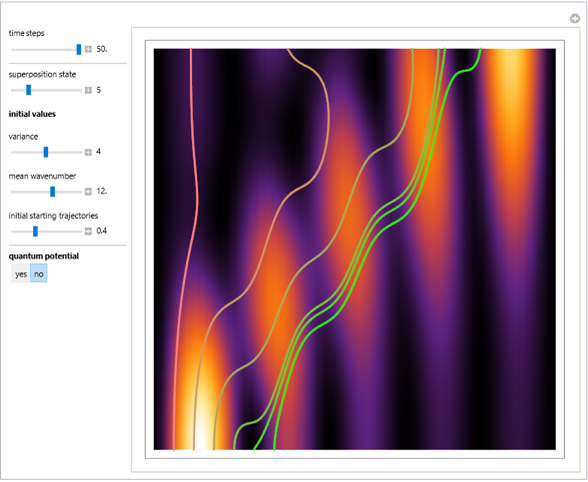
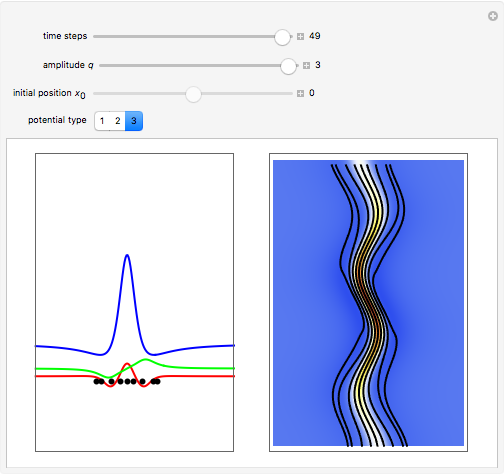
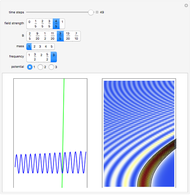
This Demonstration simulates the triple‐slit experiment numerically according to the causal interpretation of David Bohm and Louis de Broglie. The slits generate three Gaussian profiles in  space, positioned at 0 and
space, positioned at 0 and  . The initial form of the unnormalized waves are
. The initial form of the unnormalized waves are  , where
, where  are the wave numbers in the
are the wave numbers in the  direction,
direction,  are the widths of the wave packets at
are the widths of the wave packets at  ,
,  are the constant phase shifts
are the constant phase shifts  and
and  ),
),  are the real-valued constants with
are the real-valued constants with  ,
,  ,
,  , and where
, and where  with
with  . In this case the total wavefunction
. In this case the total wavefunction  is the superposition of the three waves
is the superposition of the three waves  , where the time evolution is to be calculated from the free Schrödinger equation (
, where the time evolution is to be calculated from the free Schrödinger equation ( ):
):  with
with  , and so on.
, and so on.
Contributed by: Klaus von Bloh (March 2013)
After work by: Michael Schmidt and Franco Selleri
Open content licensed under CC BY-NC-SA
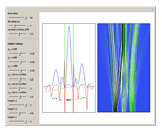
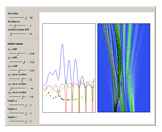
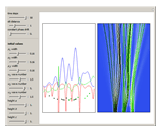
Snapshots
Details
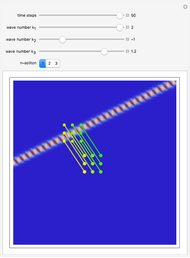
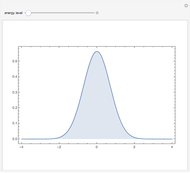
In the program, if you increase PlotPoints, AccuracyGoal, PrecisionGoal, and MaxSteps, the results will be more accurate. The starting positions of the particles are linearly distributed around the peaks of the wave density at  . Furthermore, the number of the particles depends on the initial squared amplitude of each unnormalized wave, which is proportional to
. Furthermore, the number of the particles depends on the initial squared amplitude of each unnormalized wave, which is proportional to  ,
,  , and
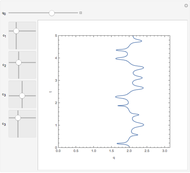
, and  . If the constant phase shift of the wave from the second slit is changed, the interference pattern and therefore the motion of the particles change significantly. The particle positions are plotted against their downscaled kinetic energy along the vertical axis.
. If the constant phase shift of the wave from the second slit is changed, the interference pattern and therefore the motion of the particles change significantly. The particle positions are plotted against their downscaled kinetic energy along the vertical axis.
The trajectories for the double slit were first numerically calculated in [1]. The effects of empty waves are discussed in [2]. For more detailed information about Bohmian mechanics, see [3].
References
[1] C. Philippidis, C. Dewdney, and B. J. Hiley, "Quantum Interference and the Quantum Potential," Il Nuovo Cimento B Series 11, 52(1), 1979 pp. 15–28. doi:10.1007/BF02743566.
[2] M. Schmidt and F. Selleri, "Empty-Wave Effects on Particle Trajectories in Triple-Slit Experiments," Foundations of Physics Letters, 4(1), 1991 pp. 1–17. doi:10.1007/BF00666413.
[3] S. Goldstein. "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy. (Mar 4, 2013)plato.stanford.edu/entries/qm-bohm.
Permanent Citation