Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Turing Snakes

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

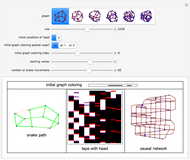
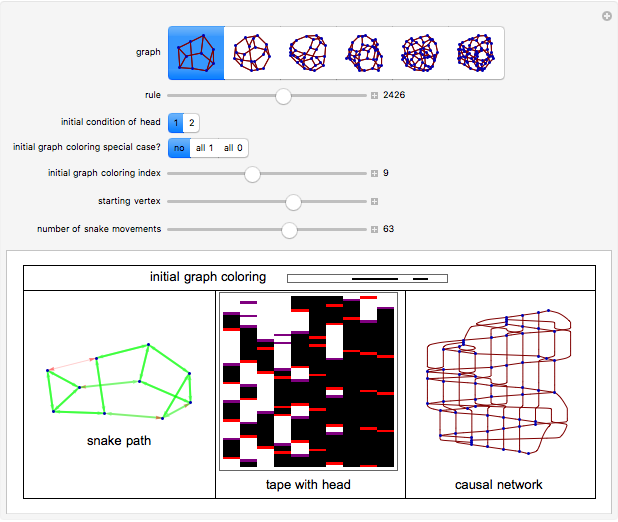
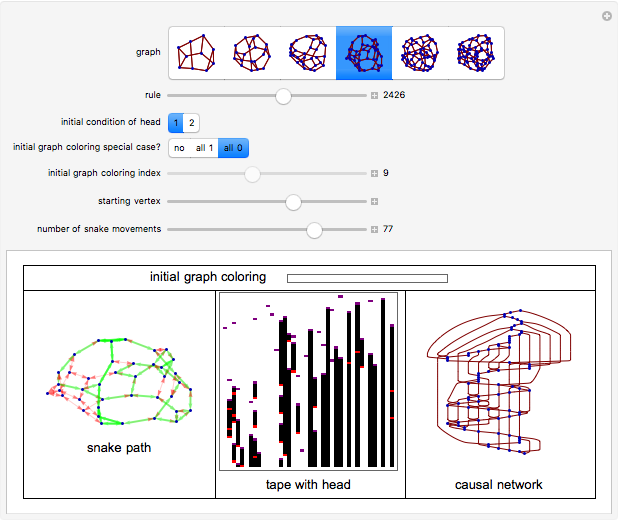
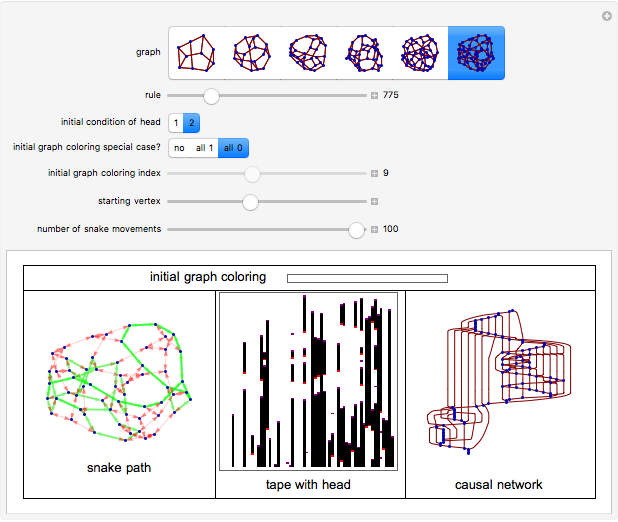
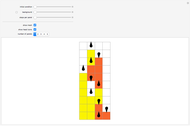
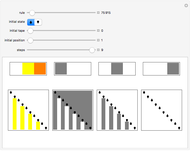
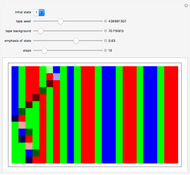
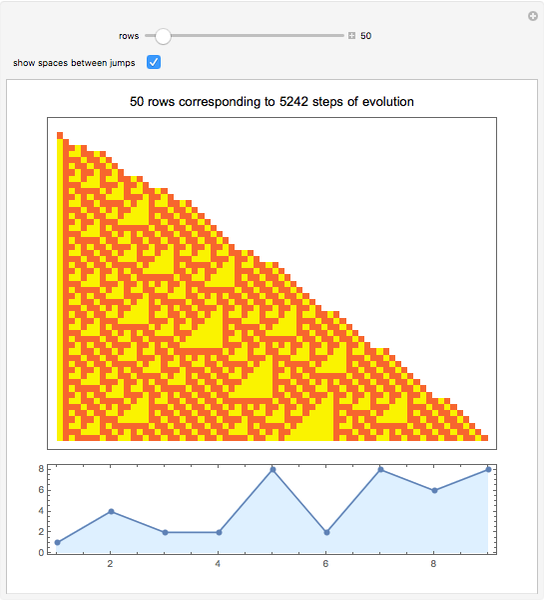
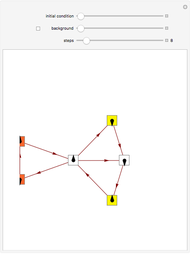
A Turing snake is a computational device similar to a Turing machine in which a "snake" with a head and tail tours a colored regular graph. As the head of the snake passes over a vertex, it measures its own internal state and the color of the vertex under its head. It uses these measurements to determine its new state, to recolor the vertex under its head, and to select which edge of the graph over which to slither. (The snake cannot coil back immediately over its own tail.)

[more]

In this Demonstration, you select which of six sample regular graphs you wish to examine, the update rule used by the Turing snake from the set of all two-state, two-color rules, the initial state of the head, the initial coloring of the graph, the vertex over which the snake's head is initially positioned, and the number of moves to be made by the snake.

The system outputs three graphics. The leftmost graphic shows the movements of the snake over the selected graph induced by the selected parameters. Edges traversed by the snake are shown in green; untraversed edges are in red. The middle graphic shows the evolution of the system on a flattened version of the graph. As with many diagrams used in A New Kind of Science, "time" goes forward as you move down the rows. A red site indicates that the head is at that site and is in state 1; a purple site indicates that the head is at that site and is in state 2. The rightmost graphic shows the causal network created by the system.

[less]

Contributed by: Seth J. Chandler (March 2011)
Suggested by: Ed Pegg Jr
Open content licensed under CC BY-NC-SA

Snapshots

Details

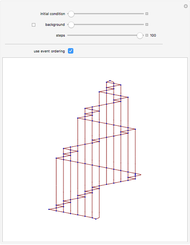
To maximize the prospect of vertices that are "close" to each other in the graphic being numbered close to each other and, thus, to facilitate a visualization of the system's evolution, a tentative version of each of the graphs is embedded as a layered directed graph. The vertices are then renumbered by sorting their vertical coordinates.

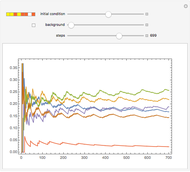
An interesting experiment would be to see which snake updating rules tend to be most efficient in causing the snake to traverse the highest proportion of graph edges. Are there rules that robustly succeed in this regard for a large number of graphs?

Although this Demonstration presents a two-state snake traversing a two-color 3-regular network, much of the code can be deployed to study more general snakes.

The pun implicit in the title is intended.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send