Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Quantitative Approach to Law of Mass Action

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

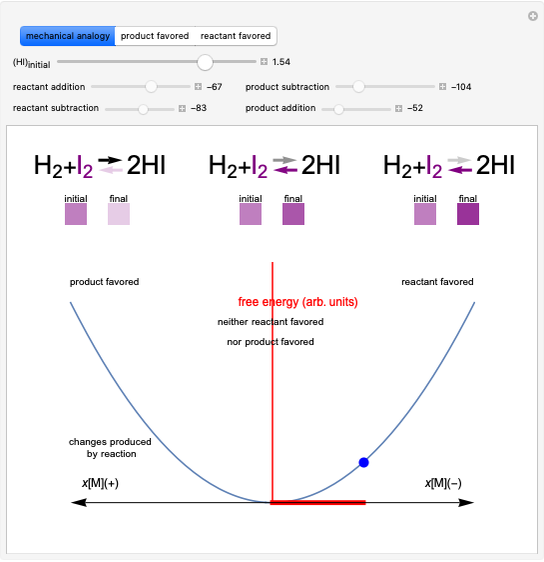
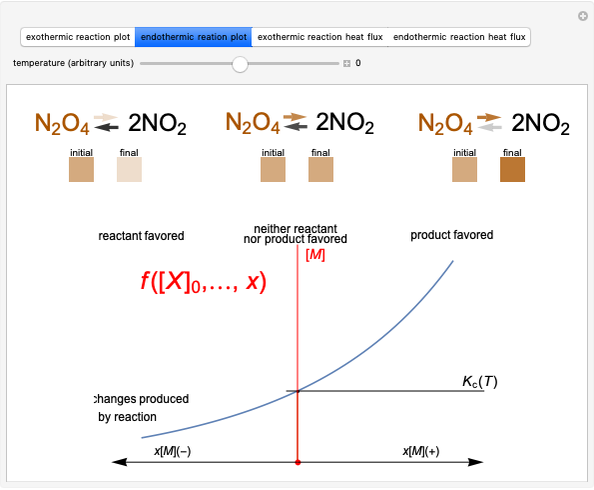
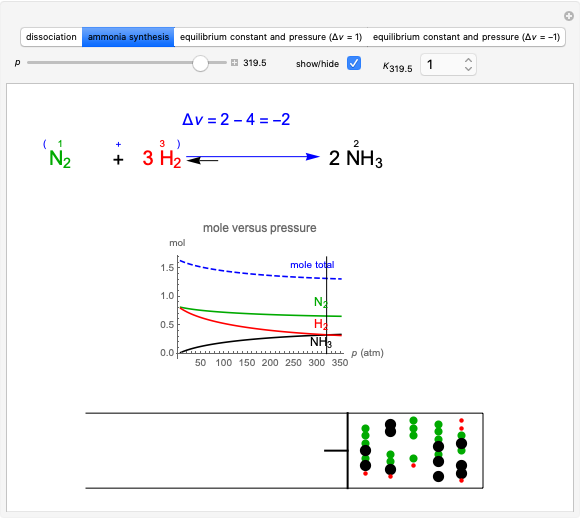
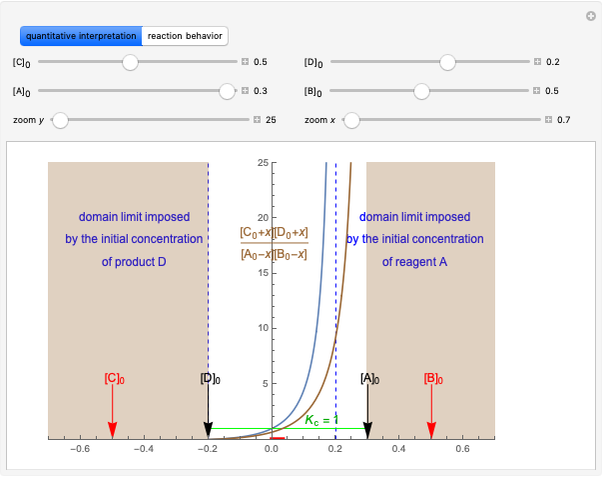
This Demonstration illustrates the law of mass action, which is an example of Le Chatelier's principle, that if a system in chemical equilibrium is disturbed it tends to change in such a way as to counteract the disturbance.

[more]

The final concentrations in a reaction are related to initial concentrations by the equation for the equilibrium constant for a generic reaction with all stoichiometric coefficients set equal to 1 and fixed temperature [1]:

.

This allows us to obtain the final concentrations by using:

, , and .

The concentrations at the equilibrium are set as:

, , and

so is equal to 1. The domain for a physically valid solution (all the final concentrations must assume positive values) is determined by and as a consequence of the solution of the system of inequalities: .

As the concentrations change, the plot is shifted (brown plot) following Le Chatelier's principle. A red line shows the magnitude of the shifting and the value.

Selecting "reaction behavior" shows the numerical values and which side is favored after altering the concentrations.

[less]

Contributed by: D. Meliga, L. Lavagnino and S. Z. Lavagnino (July 2020)
Open content licensed under CC BY-NC-SA

Snapshots

Details

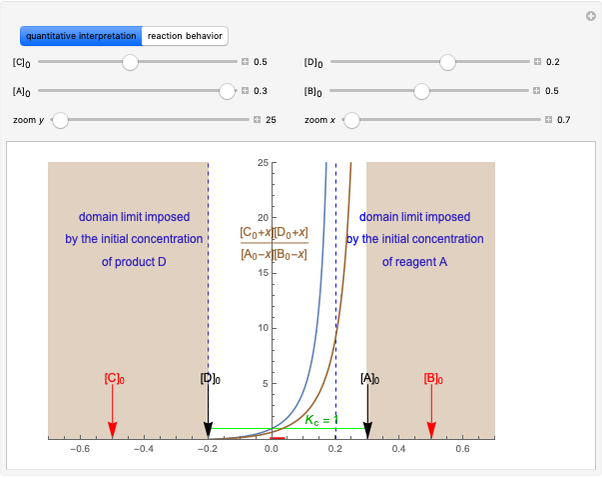
Snapshot 1: system at the equilibrium; the initial concentration fulfils the equilibrium constant equation so there is no variation

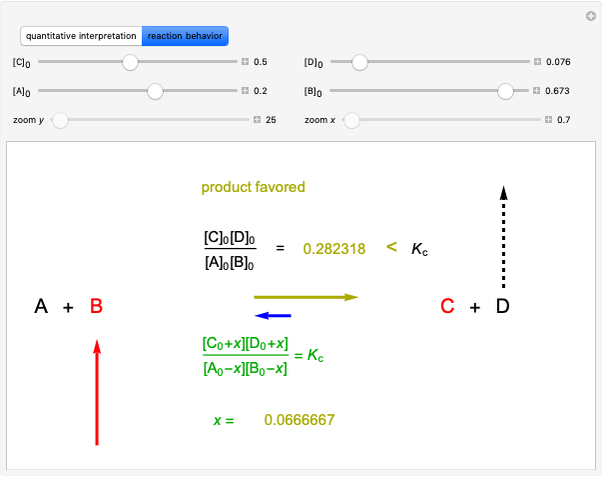
Snapshot 2: Le Chatelier's principle: raising one reactant concentration and lowering one product concentration in the equilibrium state causes a shift toward the side of products ()

Snapshot 3: raising reactant concentrations and lowering product concentrations in the equilibrium state causes a shift toward the side of products ()

References

[1] C. H. P. Lupis, Chemical Thermodynamics of Materials, New York: North-Holland, 1983.

[2] S. Z. Lavagnino. Chemical Equilibrium [Video]. (Jun 25, 2020) www.youtube.com/watch?v=TDBQOF7M-W8&list=PLswwssc6Q2yac7AM3x5UjmesLQaye-xMP&index=3.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send