Details

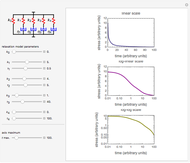
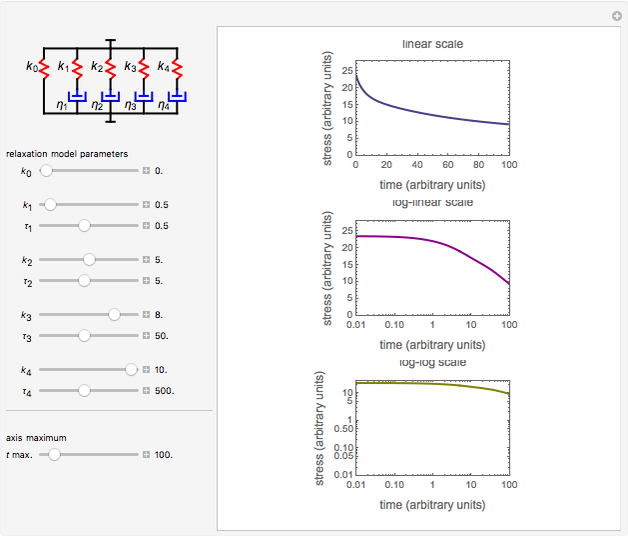
Snapshot 1: liquid dominated by short relaxation times

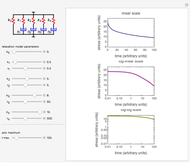
Snapshot 2: liquid dominated by long relaxation times

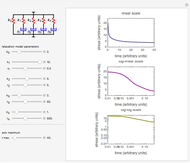
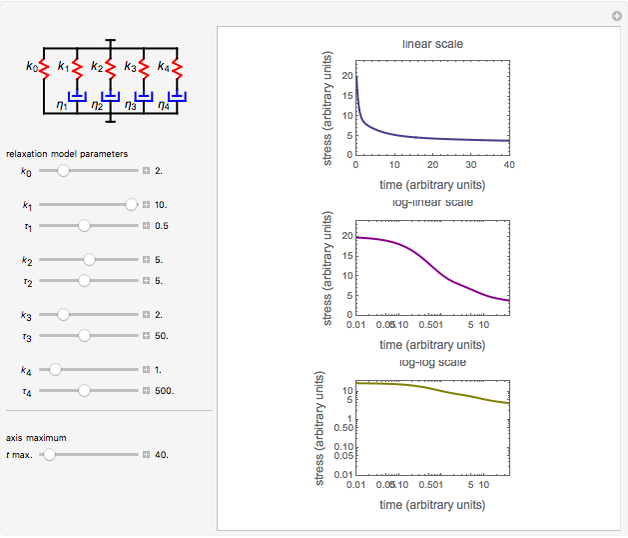
Snapshot 3: solid dominated by short relaxation times

Snapshot 4: solid dominated by long relaxation times

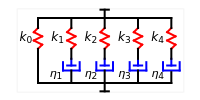
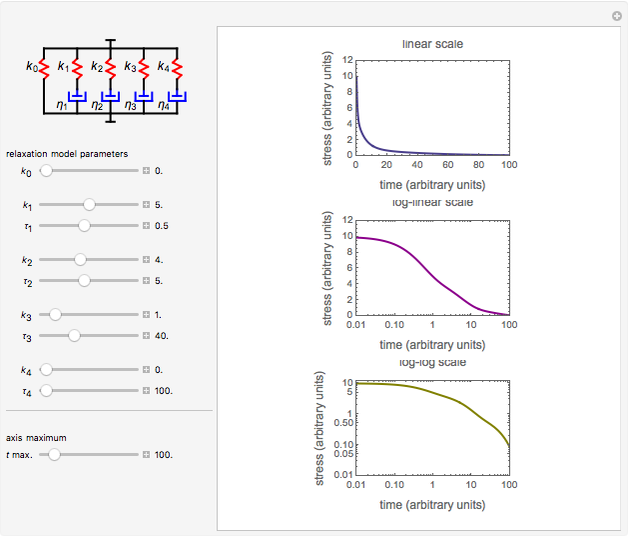
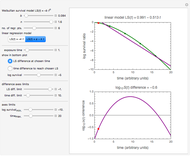
This Demonstration generates stress relaxation curves produced by a discrete Maxwell model having a spring in parallel to four Maxwell elements with increasing relaxation times subjected to a unit strain. The model’s relaxation equation is , where the are the elements' elastic components’ (springs’ moduli) and the their relaxation times, . The free spring is equivalent to a Maxwell element with . According to this model, is positive for a viscoelastic solid and zero for a liquid.

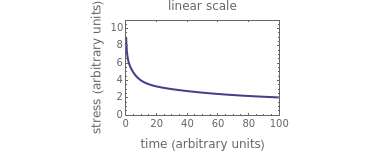
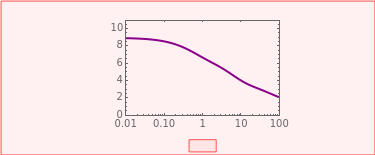
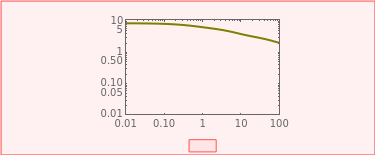
Use sliders to enter the elements’ parameter values and the experiment’s duration, . The corresponding relaxation curve is drawn on linear coordinates (top), linear-logarithmic coordinates (center), and as a log-log plot (bottom).

References

[1] D. R. Bland, The Theory of Linear Viscoelasticity, New York: Pergamon Press, 1960.

[2] W. N. Findley, J. S. Lai, and K. Onaran, Creep and Relaxation of Nonlinear Viscoelastic Materials, New York: North–Holland Publishing Company, 1976.