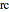Insurance and Precautions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
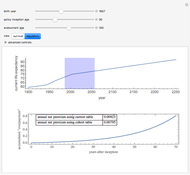
A prospective insured facing an insurable risk generally chooses how much insurance to purchase against the risk and the level of precautions to take to avoid the risk materializing. Increasing the precautions reduces the probability of a potentially costly accident but costs money. Increasing the insurance reduces the loss to the insured from an accident but increases premiums. The insurer attempts to control the insured's choices due to the twin threats of moral hazard—reduced precautions by the insured after purchasing large amounts of insurance—and adverse selection—increased purchase of insurance by the insured who suspects, usually correctly, that the risk is beyond that reflected in the premium. The insurer generally addresses moral hazard by assessing, after an accident, whether the insured has been "grossly negligent" or failed to meet some other contractually specified standard. If so, the insurer refuses to indemnify the insured. The insurer generally addresses adverse selection (and also the potential for heightened moral hazard) through its underwriting processes by refusing to issue policies where the amount of insurance requested is excessive. Neither of these conditions can generally be enforced with perfect accuracy. Increasing the accuracy of determining whether these conditions have been satisfied also costs money.
[more]
Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The variables used in the formulas employed by this Demonstration are defined as follows:
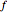 is the baseline probability of an accident, that is, the probability of an accident if the insured takes no precautions against it.
is the baseline probability of an accident, that is, the probability of an accident if the insured takes no precautions against it.
 is a measure of the risk aversion of the insured, where higher levels of
is a measure of the risk aversion of the insured, where higher levels of  correspond to higher levels of risk aversion; the insured is assumed to have a constant absolute level of risk aversion (CARA).
correspond to higher levels of risk aversion; the insured is assumed to have a constant absolute level of risk aversion (CARA).
 is the maximum amount of insurance that may lawfully be purchased.
is the maximum amount of insurance that may lawfully be purchased.
 is the accuracy with which it is determined whether the amount of insurance purchased exceeded the maximum.
is the accuracy with which it is determined whether the amount of insurance purchased exceeded the maximum.
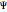 is the minimum amount of precautions that the insured must take before the insured has a right to payment in the event of an accident.
is the minimum amount of precautions that the insured must take before the insured has a right to payment in the event of an accident.
 is the accuracy with which it is determined whether the amount of precautions taken was under the minimum.
is the accuracy with which it is determined whether the amount of precautions taken was under the minimum.
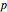 is the price per unit of insurance.
is the price per unit of insurance.
 is the price per unit of precaution.
is the price per unit of precaution.
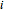 is the amount of insurance purchased.
is the amount of insurance purchased.
 is the level of precautions taken.
is the level of precautions taken.
The model is scaled so that an accident causes a loss of 1.
The utility of the insured is 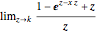 . The function of
. The function of  ,
, 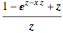 , has the property that equals 1 at 1, that its derivative at 1 is 1, and that, for
, has the property that equals 1 at 1, that its derivative at 1 is 1, and that, for 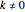 the ratio of its first derivative to its second derivative (absolute risk aversion) is equal to
the ratio of its first derivative to its second derivative (absolute risk aversion) is equal to 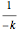 .
.
The expected utility of the insured is computed based on the mathematical expectation of a transformed distribution: 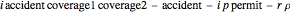 , where
, where  ,
, 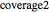 , and
, and 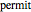 are random variables. The random variable
are random variables. The random variable  is distributed according to a Bernoulli distribution with a parameter usually equal to the cumulative distribution function of a normal distribution with mean
is distributed according to a Bernoulli distribution with a parameter usually equal to the cumulative distribution function of a normal distribution with mean 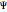 and standard deviation
and standard deviation  evaluated at
evaluated at  , the level of precautions taken. When the standard deviation
, the level of precautions taken. When the standard deviation  of this normal distribution goes to the limit of zero, the Bernoulli parameter is 1 if the level of precautions equals or exceeds the "standard" of
of this normal distribution goes to the limit of zero, the Bernoulli parameter is 1 if the level of precautions equals or exceeds the "standard" of 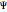 and is 0 otherwise. The random variable
and is 0 otherwise. The random variable 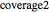 is subject to a somewhat similar distribution. It is distributed according to a Bernoulli distribution with a parameter usually equal to the cumulative distribution function of a normal distribution with mean
is subject to a somewhat similar distribution. It is distributed according to a Bernoulli distribution with a parameter usually equal to the cumulative distribution function of a normal distribution with mean  and standard deviation
and standard deviation  , evaluated at
, evaluated at 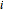 , the level of insurance purchased. When the standard deviation
, the level of insurance purchased. When the standard deviation  of this normal distribution goes to the limit of zero, the Bernoulli parameter is 0 if the level of precautions equals or exceeds the "standard" of
of this normal distribution goes to the limit of zero, the Bernoulli parameter is 0 if the level of precautions equals or exceeds the "standard" of  and is 0 otherwise. The random variable
and is 0 otherwise. The random variable 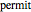 (used to prevent negative insurance) is distributed according to a Bernoulli distribution with parameter 1 if
(used to prevent negative insurance) is distributed according to a Bernoulli distribution with parameter 1 if 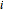 , the level of insurance purchased, is greater than 1 and a parameter of zero otherwise.
, the level of insurance purchased, is greater than 1 and a parameter of zero otherwise.
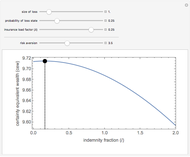
The certainty equivalent wealth of the insured is the inverse of its expected utility  , where
, where 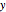 is expected utility. The certainty equivalent wealth is the amount of money that, if held with absolute certainty, would yield the insured the same expected utility as the "lottery" it faces as a result of the dependence of its utility on random variables. Use of limits is necessary to address cases where risk aversion is zero or one.
is expected utility. The certainty equivalent wealth is the amount of money that, if held with absolute certainty, would yield the insured the same expected utility as the "lottery" it faces as a result of the dependence of its utility on random variables. Use of limits is necessary to address cases where risk aversion is zero or one.
Many of the slider controls have nonlinear responses in order to gain the greatest "resolution" within the zones of interest while providing for the controls to take on relatively extreme values. This interface methodology can be used in conjunction with slider zoom to provide even greater resolution.
Tooltips on the controls and table elements of the output provide additional information.
The insurer may also prevent excessive insurance purchases by declining to pay or limiting the amount it will pay if it discovers that the amount of insurance the insured has purchased is excessive. Coordination provisions in an insurance contract, such as those requiring pro rata payment in the event of multiple insurance against the same event, provide one vehicle whereby the insurer attempts to prevent excessive purchase. See J. W. Stempel, Stempel on Insurance Contracts, 3rd. ed., 2007. A more complex approach to the situation modeled in this Demonstration would permit the insurer to use both conventional underwriting and "post-claims" underwriting to determine whether the insured had purchased excessive insurance. Such post-claims underwriting might encompass assessments after an accident whether the insured, given other insurance the insured might have in place, had purchased insurance that resulted in being better off after an accident than if no accident occurred.
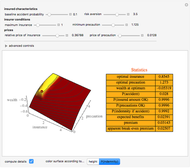
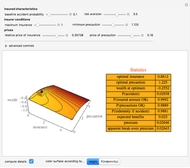
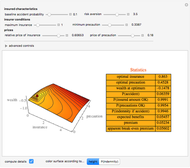
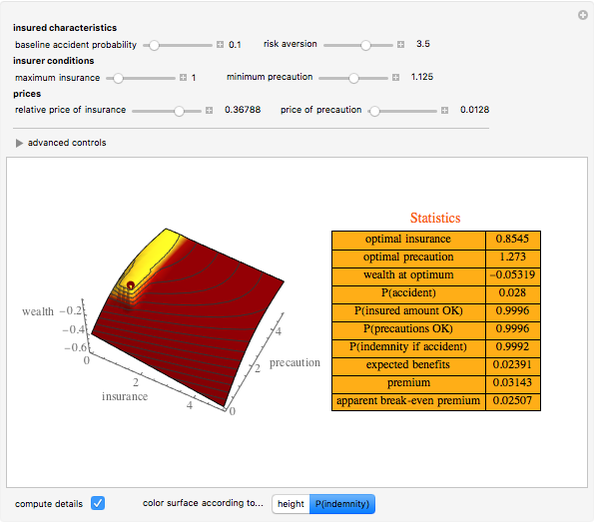
Snapshot 1: the surface is colored according to indemnity probability rather than certainty equivalent wealth
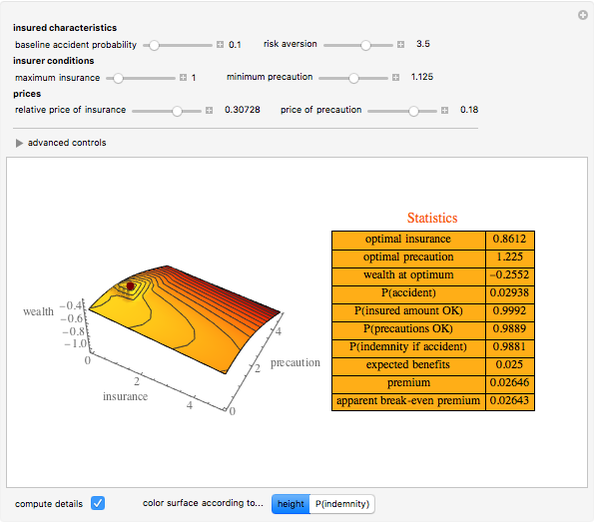
Snapshot 2: a high price of precautions relative to precaution conditions results in purchase of no insurance
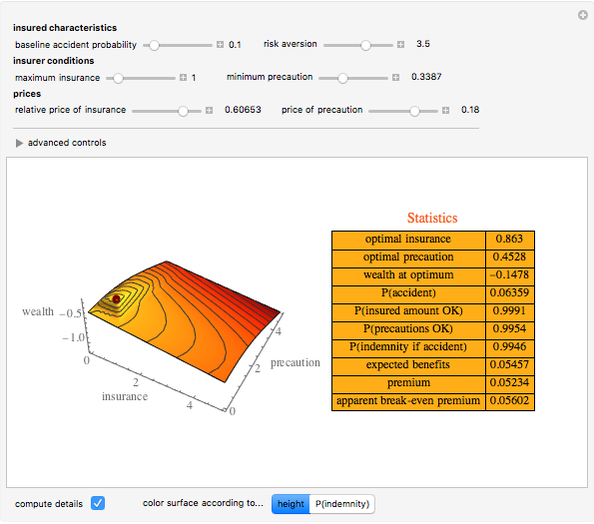
Snapshot 3: a reduction in the precaution condition permits purchase of insurance even when precautions are costly
Snapshot 4: use of advanced controls shows an effect of high costs in accurately determining whether the precaution condition has been satisfied
Snapshot 5: an insured with a high baseline risk relative to the premium purchases a large amount of insurance and takes minimal precaution where the precaution condition is low
Snapshot 6: an insured with a high baseline risk relative to the premium purchases no insurance and takes high precautions where the precaution condition is high
Snapshot 7: an insured with a low baseline risk relative to the premium charged purchases no insurance but takes high levels of precaution (well beyond what the insurer would have required)
Permanent Citation