Parameterizing Mathews versus Eldridge

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The United States Supreme Court has set forth a test for determining the constitutional adequacy of the process by which government action adversely affects someone's life, liberty, or property. In Mathews v. Eldridge, the Court required consideration of three factors: (1) the private interest that will be affected by the official action; (2) (a) the risk of an erroneous deprivation of such interest through the procedures used and (b) the probable value, if any, of additional or substitute procedural safeguards; and (3) the government's interest, including the function involved and the fiscal and administrative burdens that the additional or substitute procedural requirement would entail.
[more]
Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
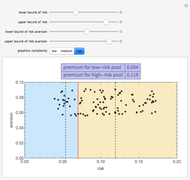
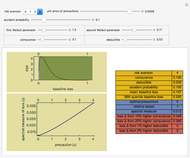
In this Demonstration, the cutoff level is described numerically by reference to some metric. This might occur where the issue in question is the person's income or assets or their score on some test. The cutoff level can also be described verbally.
The text of Mathews v. Eldridge may be found here.
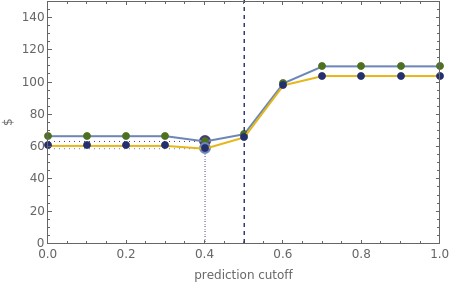
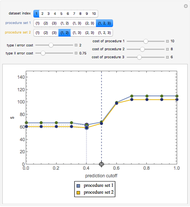
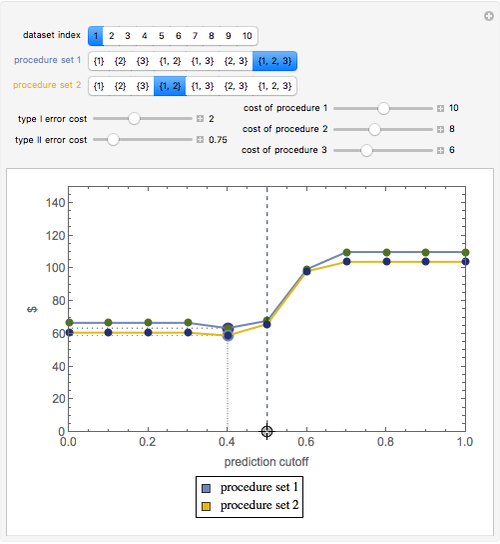
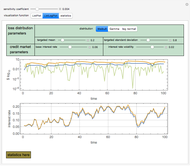
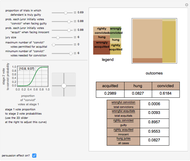
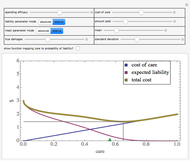
Snapshot 1: The initial settings of the Demonstration. The minimum total costs of procedure set 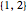 are less than the minimum total costs of procedure set
are less than the minimum total costs of procedure set 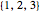 even though, as shown from the tooltips associated with the minimum points, procedure set
even though, as shown from the tooltips associated with the minimum points, procedure set 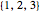 is slightly more accurate. Notice that both procedure sets do best when there is a safety margin: the prediction has to be substantially worse than the actual cutoff before the government takes adverse action against the person.
is slightly more accurate. Notice that both procedure sets do best when there is a safety margin: the prediction has to be substantially worse than the actual cutoff before the government takes adverse action against the person.
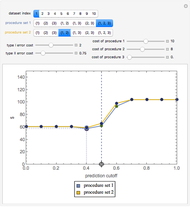
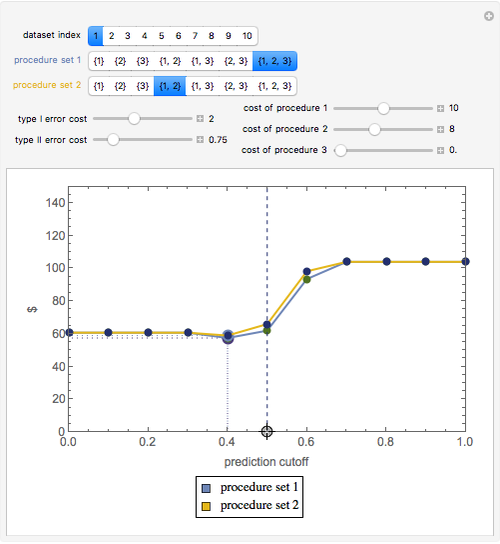
Snapshot 2: The initial settings of the Demonstration modified so that the costs of procedure 3 are zero. Now procedure set 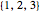 is slightly less costly than procedure set
is slightly less costly than procedure set 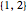 .
.
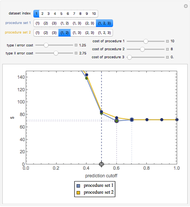
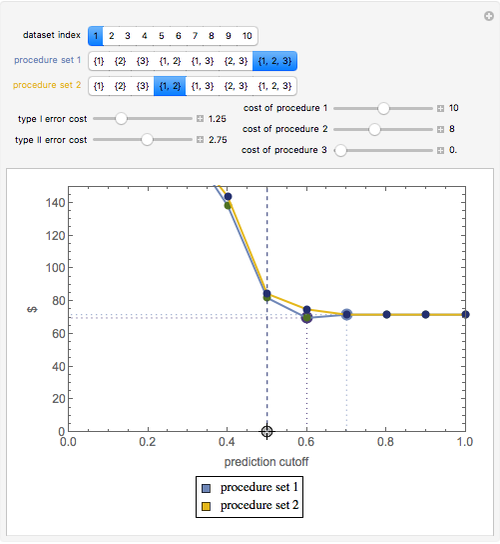
Snapshot 3: The initial settings of the Demonstration modified so that the costs of procedure 3 are zero and type I error costs are lower and type II error costs are higher. Now procedure set 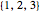 is somewhat better than procedure set
is somewhat better than procedure set 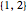 but both should employ negative safety margins, that is, authorizing adverse action against the person even when their predicted score is somewhat higher than the actual cutoff.
but both should employ negative safety margins, that is, authorizing adverse action against the person even when their predicted score is somewhat higher than the actual cutoff.
Snapshot 4: The initial settings of the Demonstration but comparing procedure set 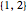 with procedure set
with procedure set 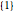 . Procedure set
. Procedure set 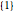 has lower total minimum costs.
has lower total minimum costs.
Snapshot 5: The initial settings of the Demonstration except that dataset 8 is used.
Permanent Citation