Magic Number Bidding

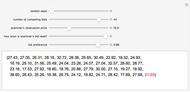
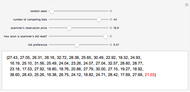
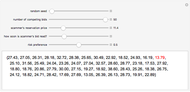
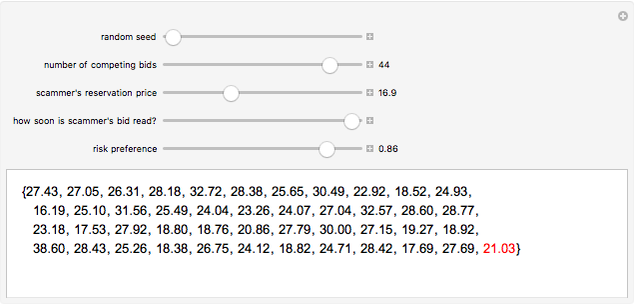
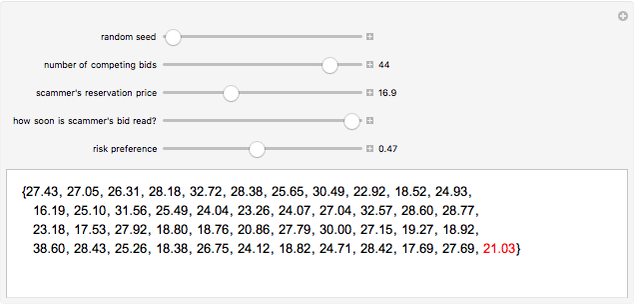
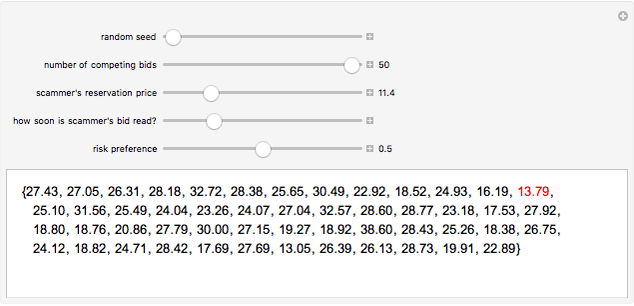
In "magic number bidding" an auctioneer colludes with a bidder ("the scammer"). The scammer secretly informs the colluding auctioneer of the scammer's reservation price, the lowest amount for which it would still be profitable to perform the work in question. The colluding auctioneer then defers "reading" the scammer's bid until last. If the scammer's reservation price is less than the minimum bid, the auctioneer says that the scammer's bid was a small amount less than the prior minimum bid. The scammer thus wins a profitable bid. If the scammer's reservation price is more than the minimum bid, the auctioneer says that the scammer's bid was something more than the minimum bid, thus ensuring that the scammer never enters a losing bid. The scammer thus profits to the extent of any positive difference between the minimum bid of other bidders and the scammer's reservation price.

This Demonstration shows a modified magic number bidding system in operation. You choose a random seed to generate the competing bids as well as the number of competing bids made. You also choose the reservation price. Unlike classic "magic number bidding," however, in which the scammer's bid is always read last—thereby providing evidence of wrongdoing—you also select when in the process you want the auctioneer to announce the scammer's bid. Announcements early in the process deflect attention from the scammer but also increase the chance that the ultimate low bid will be sandwiched above the scammer's reservation price and the scammer's bid, thereby costing the scammer a profitable contract. You also choose where between the scammer's reservation price and the minimum bid thus far the scammer wants to bid. Scammers with high risk preference will bid near the minimum bid thus far—the scammer may lose the bid, but if they win it will be far above the reservation price. Scammers with low risk preference will bid near their reservation price—they will win more auctions but will make less profit on winning bids. The Demonstration responds to the chosen parameters with the sequence of bids. Winning scammer bids are colored green. Losing scammer bids are colored red.