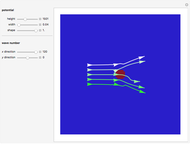
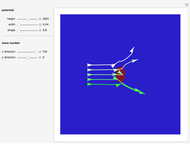
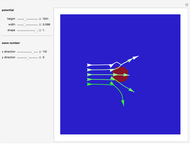
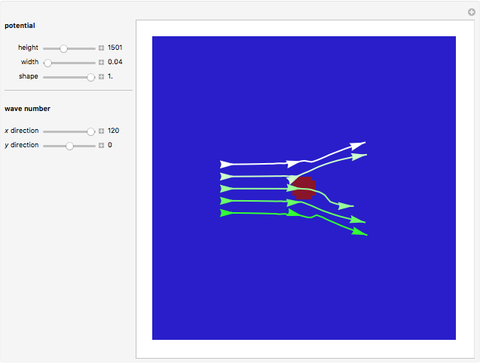
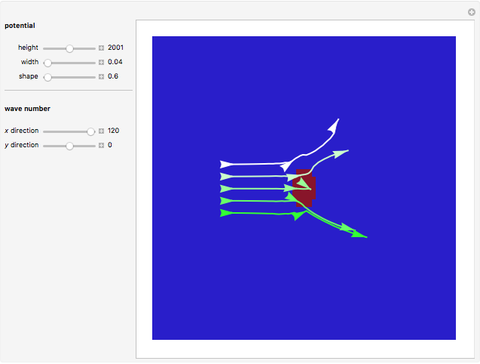
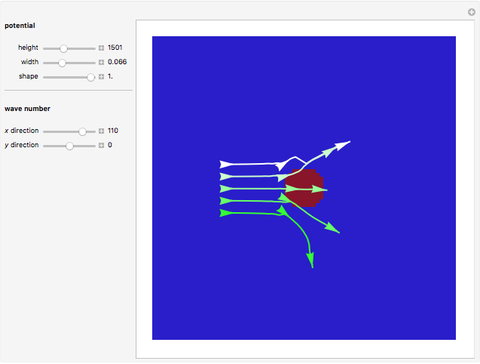
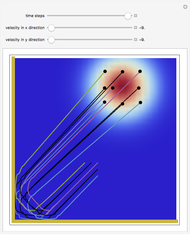
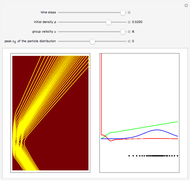
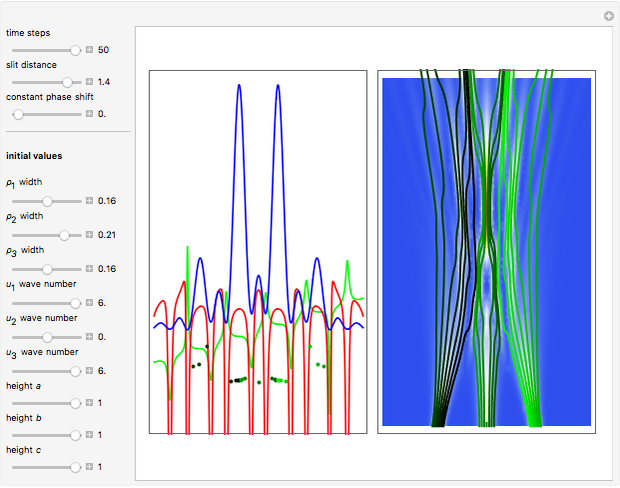
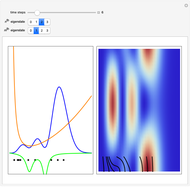
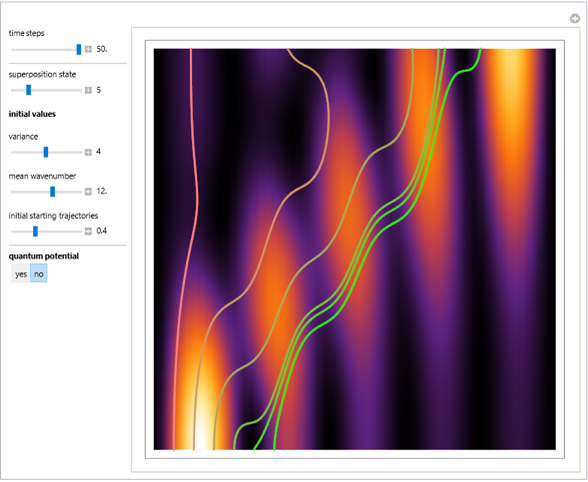
This Demonstration shows trajectories of a beam of quantum particles scattered by a stationary obstacle with variable potential height and shape. The formalism of the quantum motion is derived from the causal interpretation of D. Bohm and L. de Broglie, in which the quantum wave generates an effective potential (a sum of obstacle and quantum potentials) that the particles follow. The initial quantum wave starts from a Gaussian state. The shape of the obstacle varies from circular to elliptical. Quantum particles passing an obstacle behave differently from classical ones, because particles that are far away from the obstacle, where the obstacle potential becomes zero, are nonetheless influenced by the quantum potential. This, in turn, causes diffraction in the motion of the distant particles. This effect is a feature of the Bohm model and it follows from interference between the quantum wave and the obstacle potential. The particles that start near the center of the obstacle are deflected much more strongly than the particles that are further away, which is roughly consistent with Rutherford scattering. When the quantum flow is sufficiently slow, the particles could enter a regime in which they behave chaotically, exhibiting nodal points, vortices, ripples, and diffraction effects of the scattered wave. In some cases one finds that in addition to reflection and transmission, there is a finite probability of a particle being trapped inside the potential for a finite time. But keep in mind that single quantum trajectories (a particle's position and momentum) can never be measured simultaneously because of the uncontrollable system-environment (detector) coupling.