Enantiomorphs of the Truncated Icosahedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
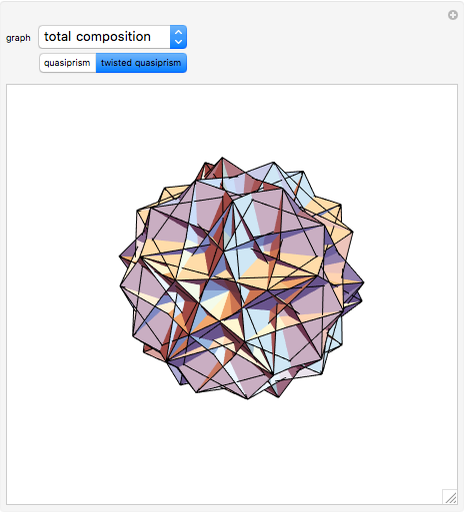
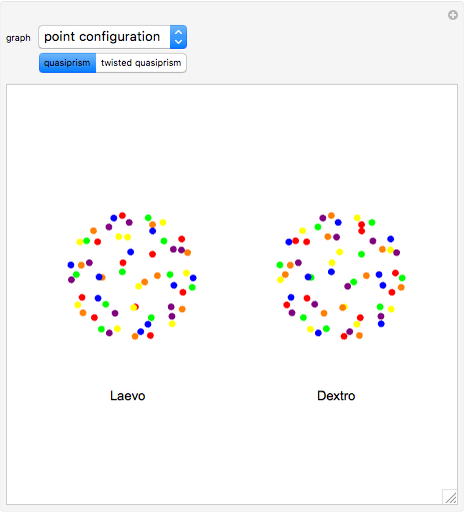
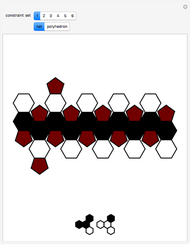
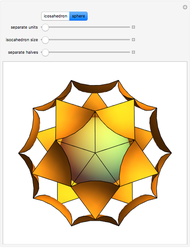
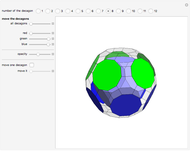
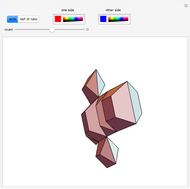
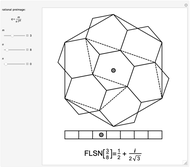
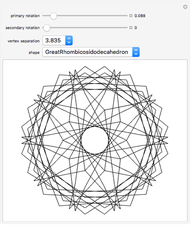
The oldest studies of polytope composition predate Kepler's Harmonices Mundi, which included the famous stella octangula. Recent studies [1] have shown the existence of a surprising number of regular compositions of regular polytopes. This Demonstration shows the composition of a regular polytope, the truncated icosahedron, from a nonregular "quasiprism". Like the dodecahedron, another polytope with icosahedral symmetry, the truncated icosahedron displays enantiomorphism. With this polytope, however, the enantiomorphism requires not only two non-equivalent halves, but additionally requires two non-equivalent compositional elements.
Contributed by: Brad Klee (August 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The composition shown above diverges from the historical trend of composing regular polytopes from other regular polytopes. These unsightly pentagonal quasiprisms remained undiscovered for thousands of years, but the enantiomorphism they display is different from that of any regular composition.
A numerical calculation of the angle of offset between pentagonal faces gives approximately 8.772 degrees. Can the offset angle be given as a ratio of  ? If not, then the projected vertices of stacked pentagonal quasiprisms will approximate a continuous circle. Alternatively, a stacking of pentagonal quasiprisms will be defined by an exact period if the angle can be rationalized.
? If not, then the projected vertices of stacked pentagonal quasiprisms will approximate a continuous circle. Alternatively, a stacking of pentagonal quasiprisms will be defined by an exact period if the angle can be rationalized.
Other polytopes must have irregular compositions as well. Do other nonregular compositions of regular polyhedra exist so that the composition uses a maximum of two nonregular polytopes? Specifically, do compositions of the icosahedron with an enantiomorphism exist? This last question may already be answered in the extensive literature about the icosahedron.
More information about uniform composition of uniform polytopes can be found on this website on polyhedra compounds, which contains useful information from [1].
Reference
[1] J. Skilling, "Uniform Compounds of Uniform Polyhedra," Mathematical Proceedings of the Cambridge Philosophical Society, 79, 1976 pp. 447–457.
Permanent Citation
"Enantiomorphs of the Truncated Icosahedron"
http://demonstrations.wolfram.com/EnantiomorphsOfTheTruncatedIcosahedron/
Wolfram Demonstrations Project
Published: August 5 2011