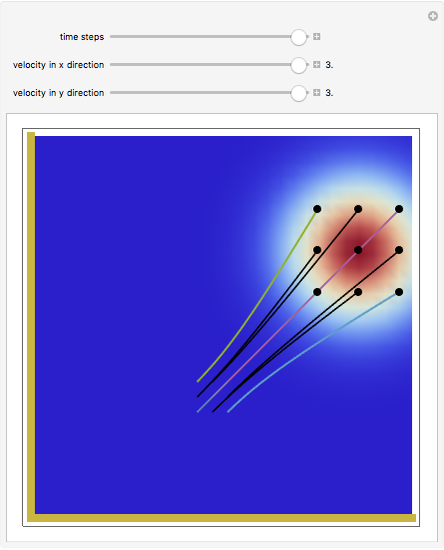
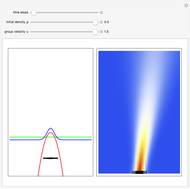
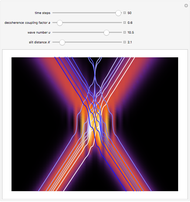
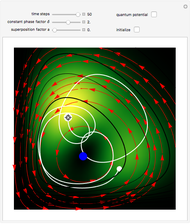
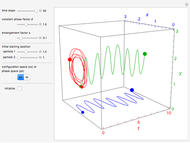
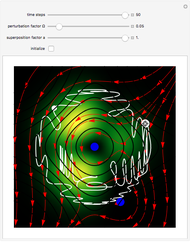
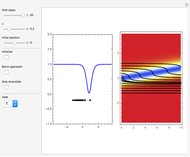
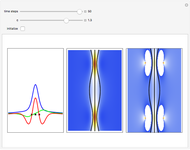
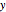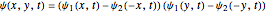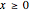This Demonstration studies a time-dependent collision of a two-dimensional wave packet with infinite wall barriers placed at right angles in the (, ) configuration space. In this case the analytic wavefunction is described by a product state: for and 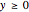, where 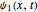and 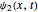are standard one-dimensional free-particle solutions of the Schrödinger equation (SE) and where 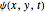is a solution of the two-dimensional SE for free particles. In the causal interpretation of quantum theory (de Broglie–Bohm theory), the trajectories of the particles could be calculated from the phase of the total wavefunction. Contrary to the motion in (, ) space the trajectories can cross space-time points in the (, 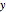) configuration space, as long as they do so at different times. 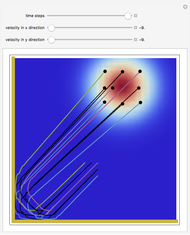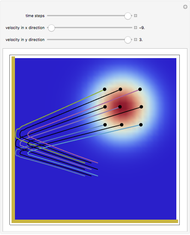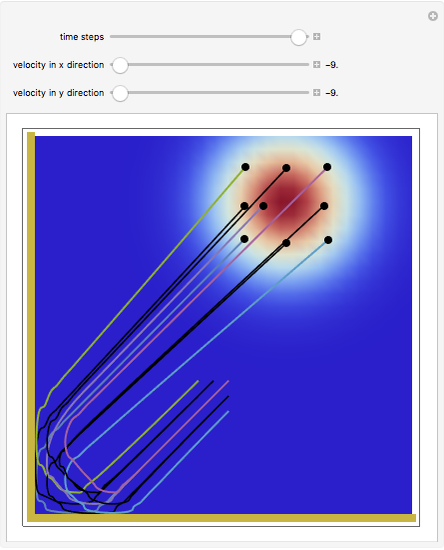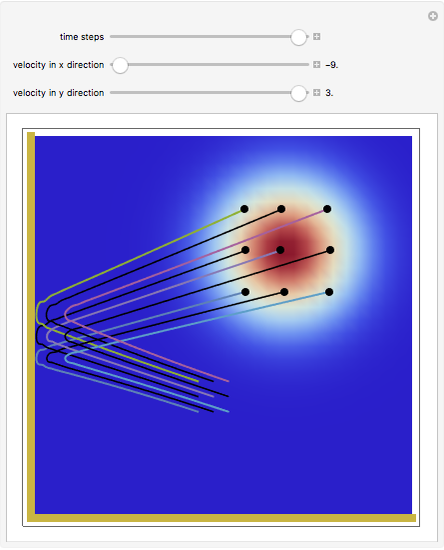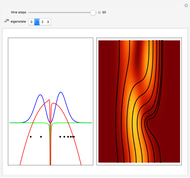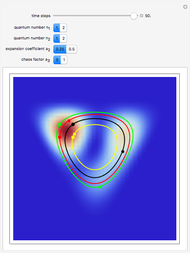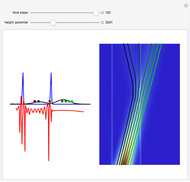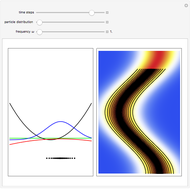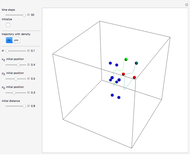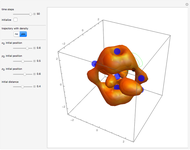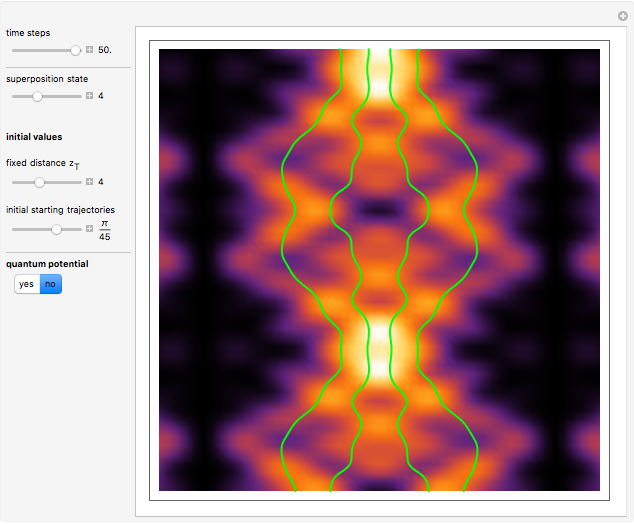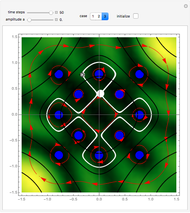Because of the product state of the wavefunction, the velocity in the direction is completely independent of the velocity in the 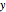direction. The graphic shows the particles, the whole paths of the particles, the squared wavefunction, and the infinite wall barriers (yellow).