Estimating Loss Functions Using Exceedance Data and the Method of Moments

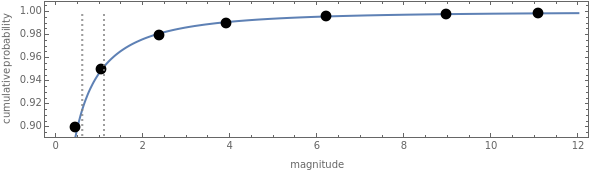
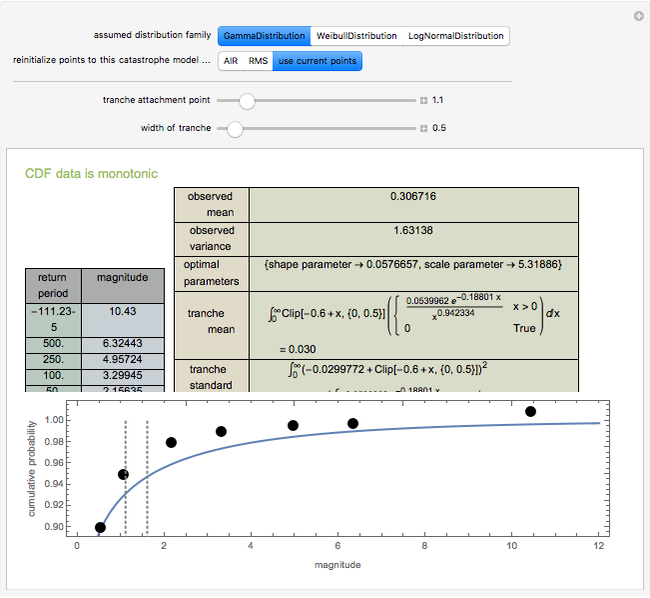
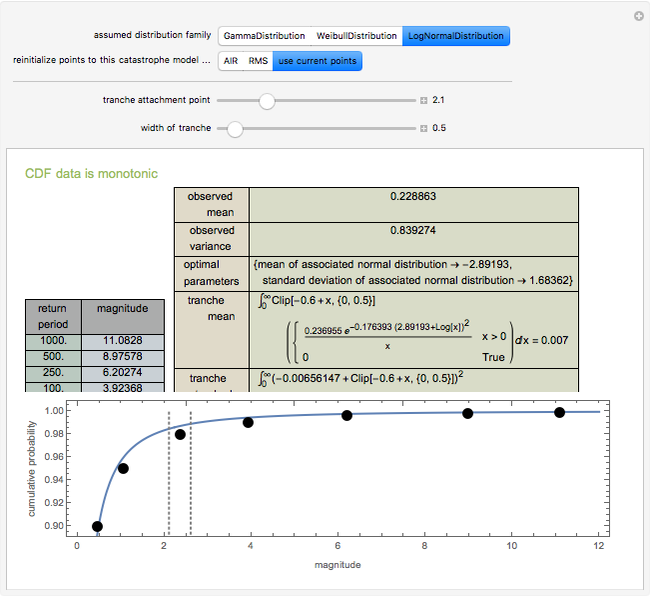
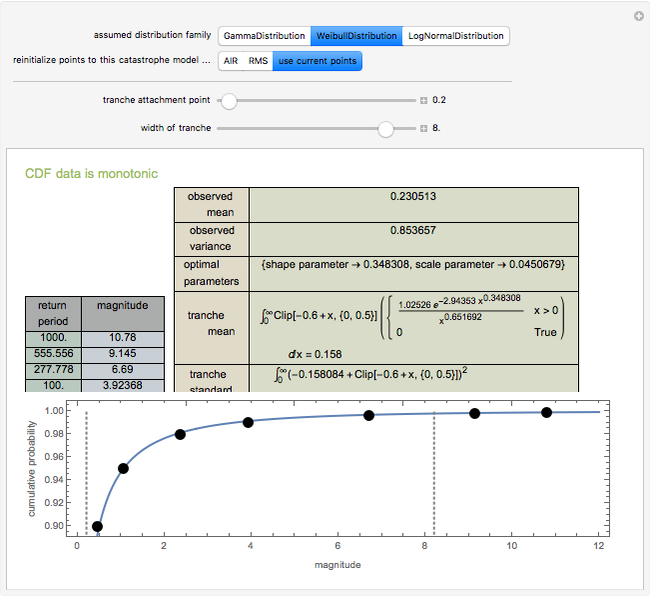
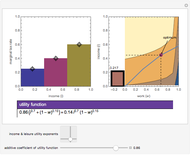
Data regarding the magnitude of catastrophes is often presented in an "exceedance table" that sets forth the number of years it would take for disasters exceeding various magnitudes to occur. This Demonstration shows how one can use exceedance data to generate a two-parameter probability distribution whose first two moments best match those observed from the data. You move locators to set a cumulative density function and determine the family of distributions for which parameters are to be estimated. The Demonstration responds by determining the parameters of that distribution whose first two moments match the observed values. A second part of the Demonstration lets you use the computed probability distribution. You move the sliders to establish a layer (or "tranche", as it is often known) for which an insurer has responsibility. An insurer might, for example, have to pay the difference between the insured's loss and 0.6, with that value clipped between zero and 0.5. In the trade, this would be called a "0.5 XS 0.6 policy". The Demonstration uses the computed probability distribution to determine the expected value and standard deviation of the payments an insurer writing such a tranche would face. These statistics are often relevant to the premium the insurer wishes to charge. A warning is provided if the cumulative density function violates monotonicity or if the algorithm for finding optimal parameters fails. You can also reinitialize the points to correspond with estimates provided by two catastrophe modelers, AIR Worldwide Corporation (AIR) and Risk Management Solutions, Inc. (RMS).