Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Graph Embedding Trajectories

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

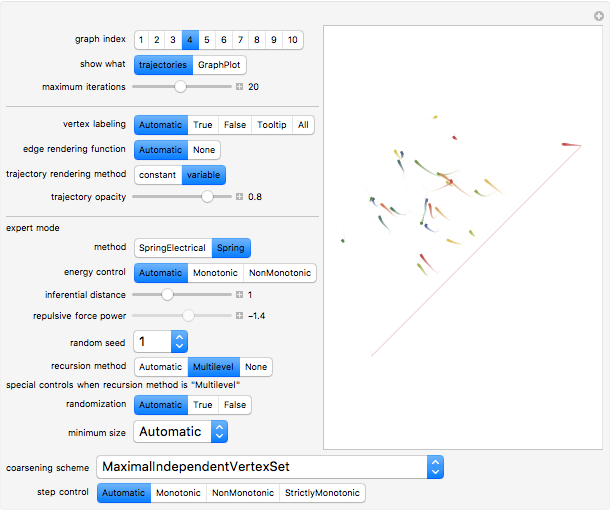
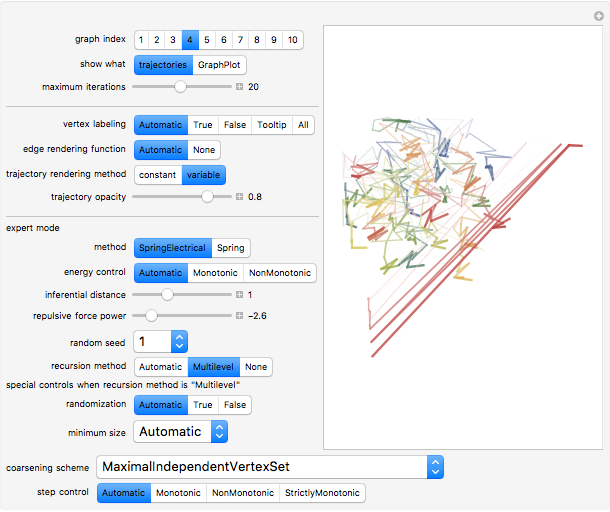
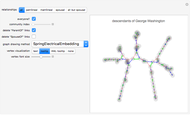
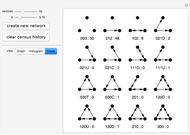
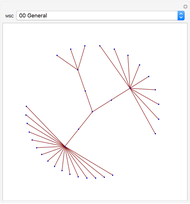
The computation of vertex coordinates for the display of a graph often proceeds through an iterative algorithm. This Demonstration shows this iterative process in two ways for 11 different random graphs. By selecting "show what" to be trajectories, you see a graphic in which the trajectory of each vertex appears as a colored line with a point at the end; each vertex has its own signature color. A second set of controls lets you control aspects of the visualization of either the GraphPlot or the trajectories. In the case of a GraphPlot, you control how the vertices are labeled and whether the edges are shown. In the case of trajectories, you control the opacity of the lines. A third set of "expert mode" controls enables advanced modifications of the iterative process using many of the options of the GraphPlot command.

Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Snapshot 1: trajectories of graph 4 with a spring electrical embedding and trajectories drawn with variable color and thickness

Snapshot 2: trajectories of graph 4 with a spring embedding and trajectories drawn with variable color and thickness

Snapshot 3: trajectories of graph 4 with a spring electrical embedding and trajectories drawn with variable color and thickness but induced by a higher absolute repulsive force power

Snapshot 4: a GraphPlot of the 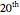iteration of graph 8

Snapshot 5: a GraphPlot of the 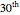iteration of graph 8

Snapshot 6: a GraphPlot of the 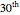iteration of graph 8 with a different starting random seed

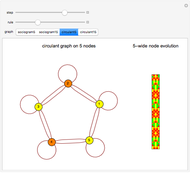
Snapshot 7: trajectories of graph 3 with a spring electrical embedding using "Multilevel" recursion and the "MaximalIndependentEdgeSet" coarsening scheme

Snapshot 8: trajectories of graph 3 with a spring electrical embedding using "Multilevel" recursion and "MaximalIndependentVertexRugeStuben" coarsening scheme

Snapshot 9: trajectories of graph 3 with a spring electrical embedding using "Multilevel" recursion and "StrictlyMonotonic" step control

The "variable" method of trajectory rendering partitions each trajectory and applies different graphic directives to each segment of the trajectory. Later "moves" within the trajectory are thicker and darker.

Information on the expert controls may be found in the "General Graph Drawing" tutorial in the standard Mathematica documentation.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send