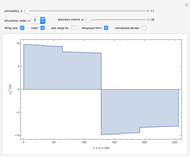
Iterations of Newton's Method for Two Nonlinear Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
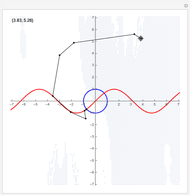
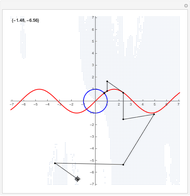
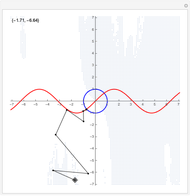
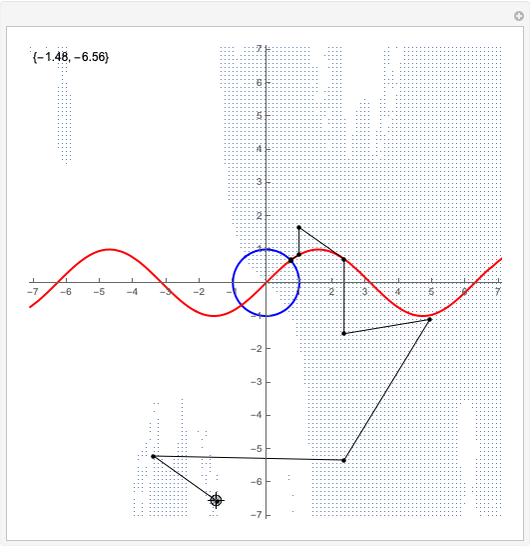
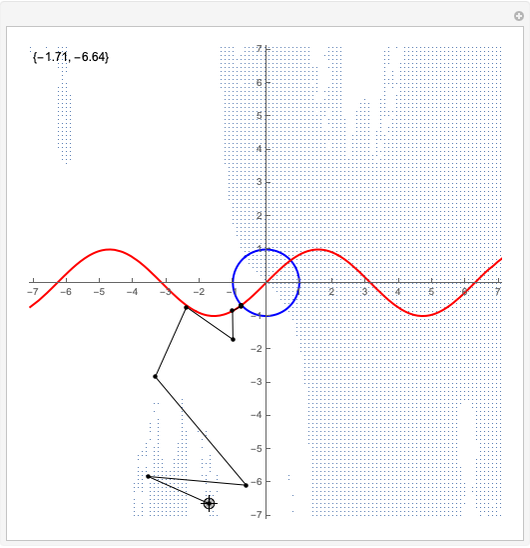
Drag the locator to see how the iterations proceed when solving a set of two nonlinear equations using Newton's method. The red and blue curves represent the points in the plane where the two equations hold. The two points of intersection of the red and blue curves are the solutions of the nonlinear system. The small light-blue points are initial points that lead to convergence to the point in the first quadrant. From the white parts of the plot, the convergence is to the point in the third quadrant.
Contributed by: Heikki Ruskeepää (January 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The snapshots show that the solution process and the point of convergence can be very different even if the starting points are very near to each other.
The two equations we consider are 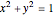 and
and 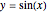 . We supply the Mathematica built-in function FindRoot with one starting point, the one shown graphically by the locator, and display it numerically in the upper-left corner. Newton's method is used to solve the nonlinear system.
. We supply the Mathematica built-in function FindRoot with one starting point, the one shown graphically by the locator, and display it numerically in the upper-left corner. Newton's method is used to solve the nonlinear system.
Permanent Citation
"Iterations of Newton's Method for Two Nonlinear Equations"
http://demonstrations.wolfram.com/IterationsOfNewtonsMethodForTwoNonlinearEquations/
Wolfram Demonstrations Project
Published: January 17 2012