Details

Subsystem A is in series with subsystem B; subsystem A has one component ) in parallel with two series components (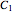, 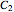); subsystem B has three parallel components 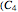, , 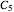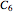). It is assumed that components 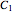, 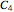have equal constant failure rate 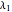, components 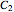, 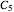have equal constant failure rate 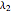, and components , 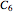have equal constant failure rate . A constant failure rate 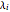implies that the times to faulure for component 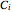are random variables that follow an exponential distribution with parameter .

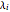Choose among three different display sets:

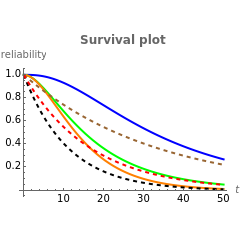
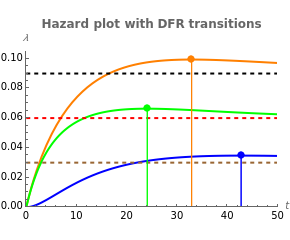
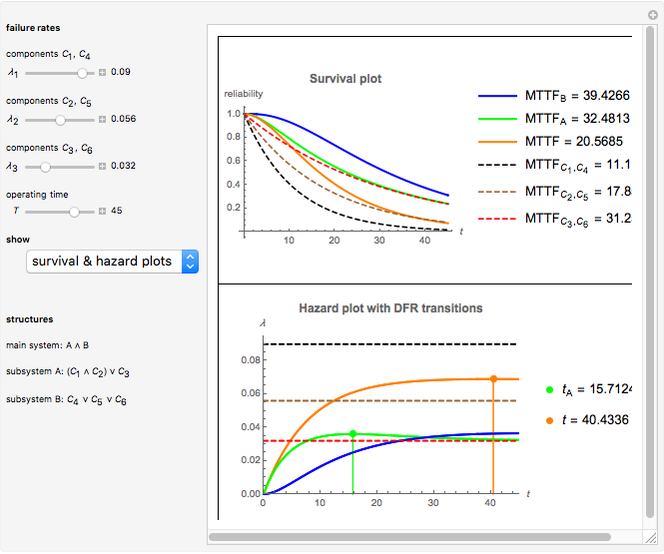
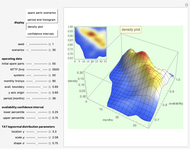
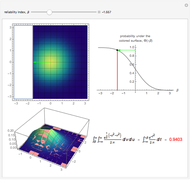
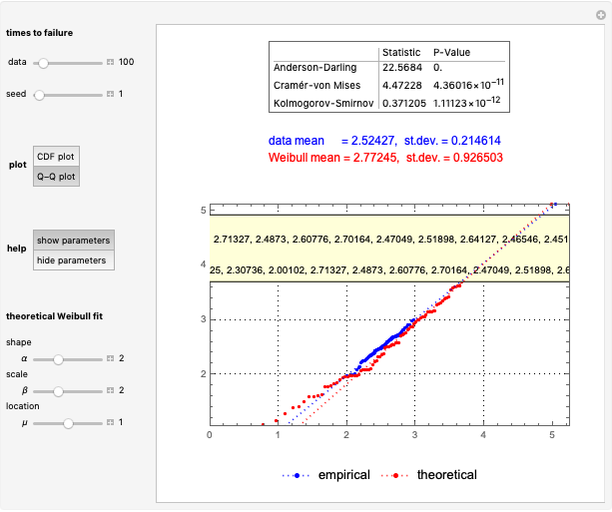
• The first display set ("survival & hazard plots") shows the survival (upper) and hazard (lower) plots for the main system, its two subsystems, and its components. It also shows the MTTF values. Notice that the main system (orange) is always less reliable than its two subsystems, because subsystem A (green) is in series with subsystem B (blue) . Also, subsystem B always has the highest reliability, because all of its components are connected in parallel (given that both subsystems, A and B, include three similar components). In cases with decreasing failure rate (DFR) transition time-points for the main system and its subsystems, time-points are indicated in the hazard plot. The dashed lines in the hazard plot indicate the constant failure rates of the components.

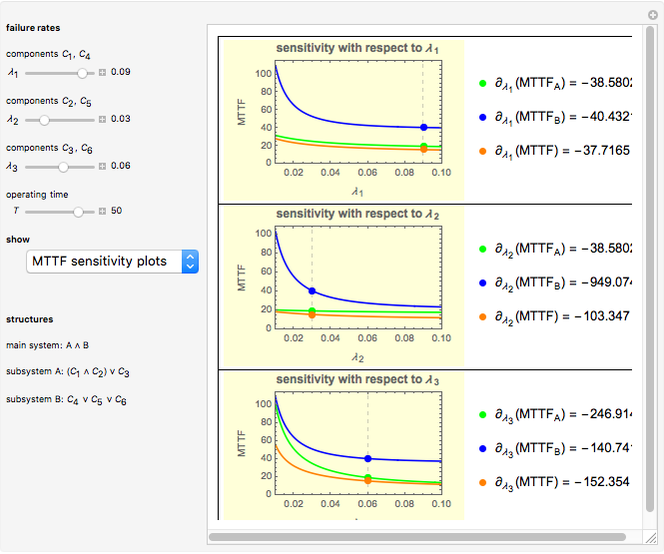
• The second display set ("MTTF sensitivity plots") shows the values of the MTTF function partial derivatives for the main system and its two subsystems at the selected failure rates 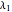, , 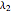and . It also shows how the MTTF functions change when each component’s failure rate varies from 0.01 to 0.10 ceteris paribus.

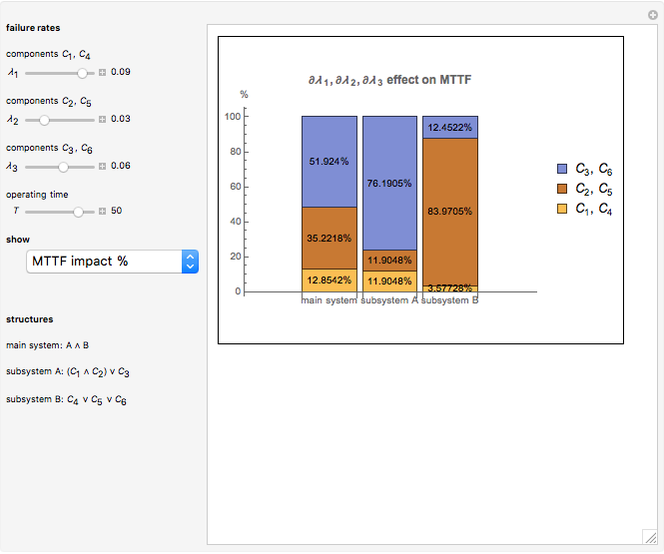
• The third display set ("MTTF impact %") illustrates the weighted effect of the selected component's failure rates marginal change on the MTTF of the main system and its two subsystems. From an engineering point of view, these weights can be used as resources for optimal allocation factors when trying to reduce the component failure rates and achieve the maximum increase in the MTTF of the subsystems or the main system.