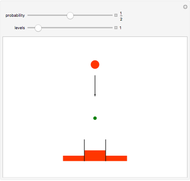
Birds on a Wire Revisited

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
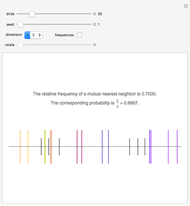
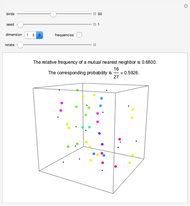
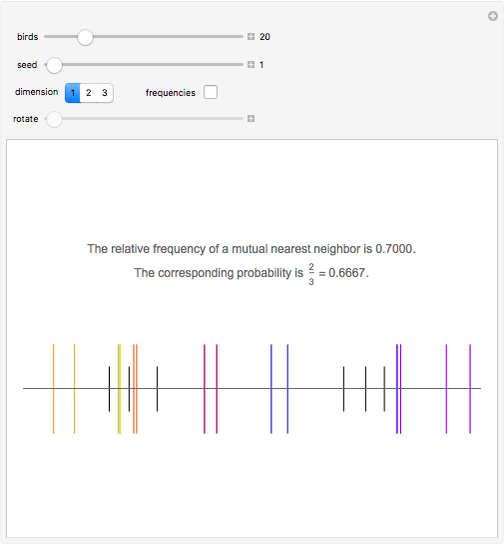
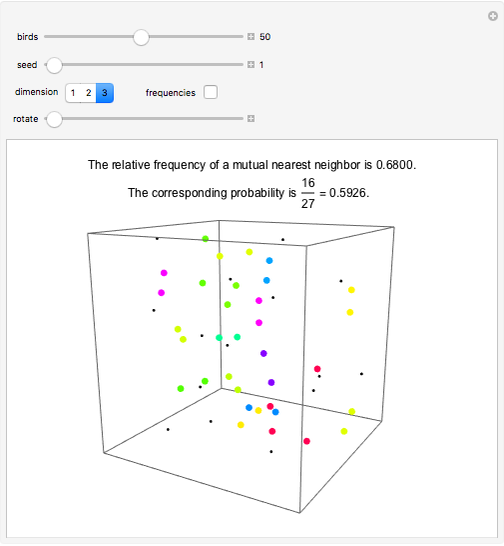
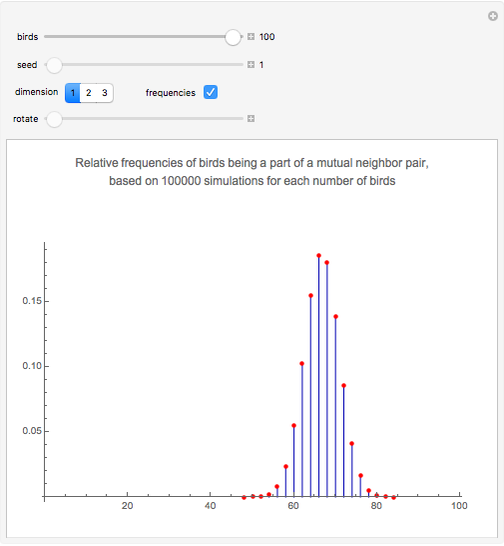
Some birds are sitting at random places on a wire. If bird B is bird A's closest neighbor and bird A is bird B's closest neighbor, then A and B are mutual nearest neighbors and form a mutual neighbor pair.
[more]
Contributed by: Heikki Ruskeepää (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
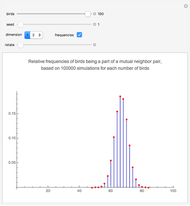
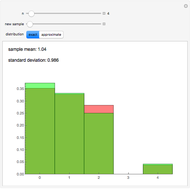
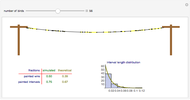
This is problem 3 in [2]. The problem originally appeared in 1978 in [4] for four birds, and asked what the probability is that a bird picked at random is looking at another bird that is looking at it. Also, what is the probability if there are more than four birds? The solution appeared the next year in [1]. In one dimension, the probability is 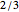 , irrespective of the number of birds! (However, for two birds the probability is, of course, one.) In two dimensions, the probability that a randomly picked point is a part of a mutual neighbor pair is
, irrespective of the number of birds! (However, for two birds the probability is, of course, one.) In two dimensions, the probability that a randomly picked point is a part of a mutual neighbor pair is 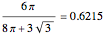 . In three dimensions, the probability is
. In three dimensions, the probability is  . As dimensions grow, the probability approaches the value
. As dimensions grow, the probability approaches the value 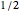 [3]. The problem is considered as a Poisson process in a Demonstration cited in the Related Links.
[3]. The problem is considered as a Poisson process in a Demonstration cited in the Related Links.
References
[1] J. Herbert, "Birds on a Wire (Solution)," Journal of Recreational Mathematics, 11(3), 1979 pp. 227–228.
[2] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton: Princeton University Press, 2008.
[3] D. K. Pickard, "Isolated Nearest Neighbors," Journal of Applied Probability, 19(2), 1982 pp. 444–449.
[4] D. P. Shine, "Birds on a Wire," Journal of Recreational Mathematics, 10(3), 1978 p. 211.
Permanent Citation
"Birds on a Wire Revisited"
http://demonstrations.wolfram.com/BirdsOnAWireRevisited/
Wolfram Demonstrations Project
Published: June 3 2012