Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

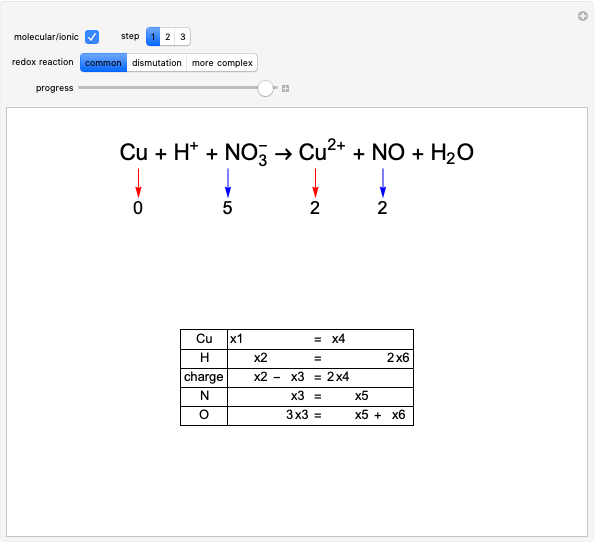
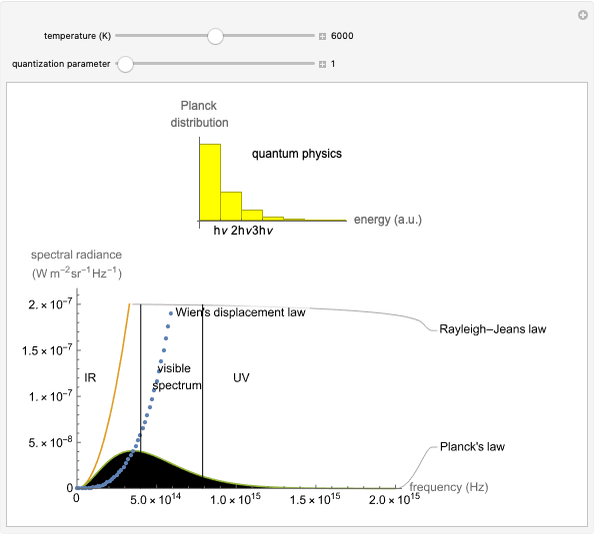
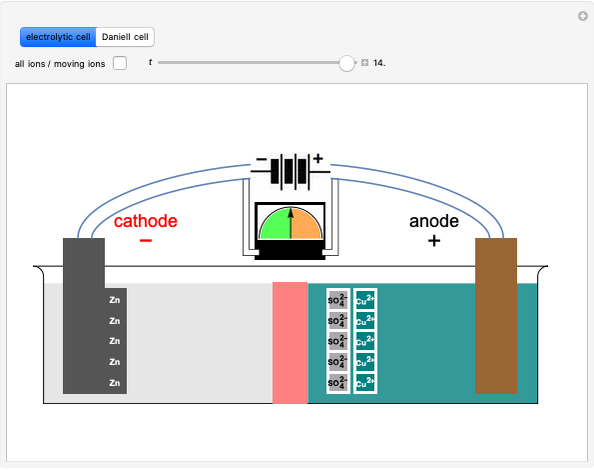
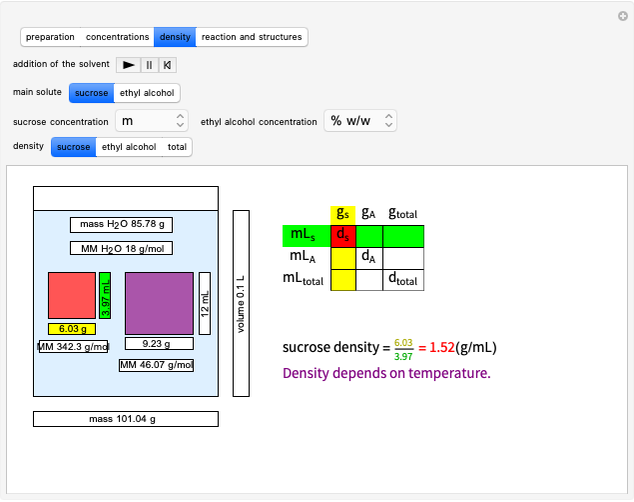
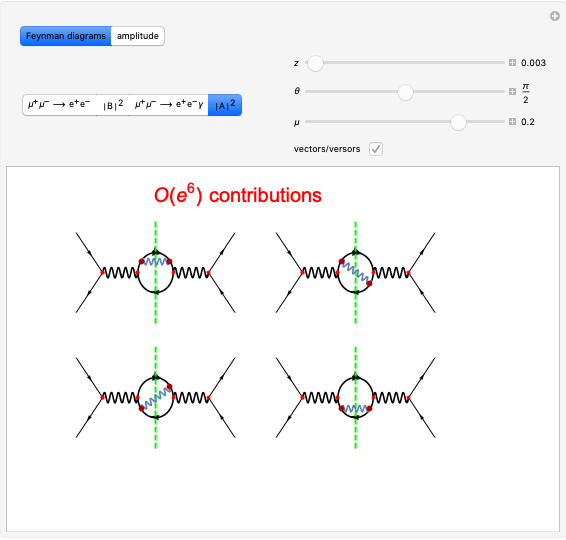
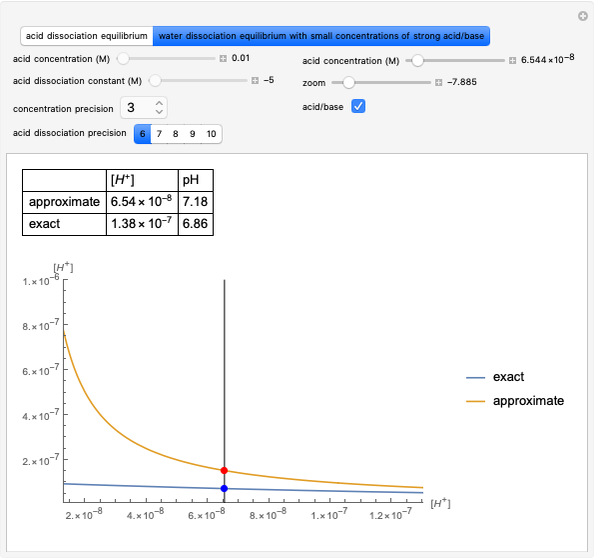
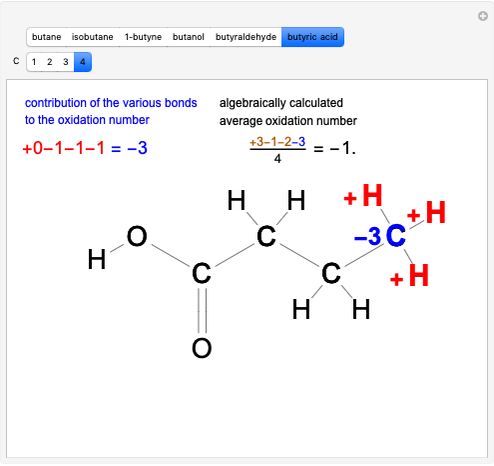
Boltzmann's Analysis of Macroscopic and Microscopic Aspects of Reversible Thermodynamic Processes

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

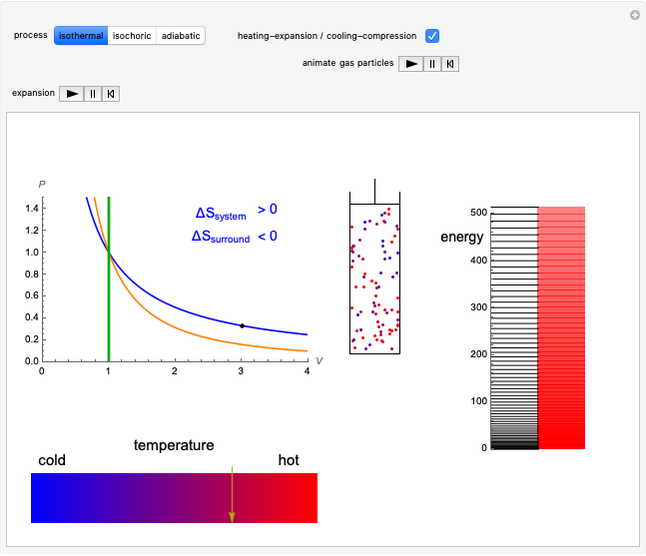
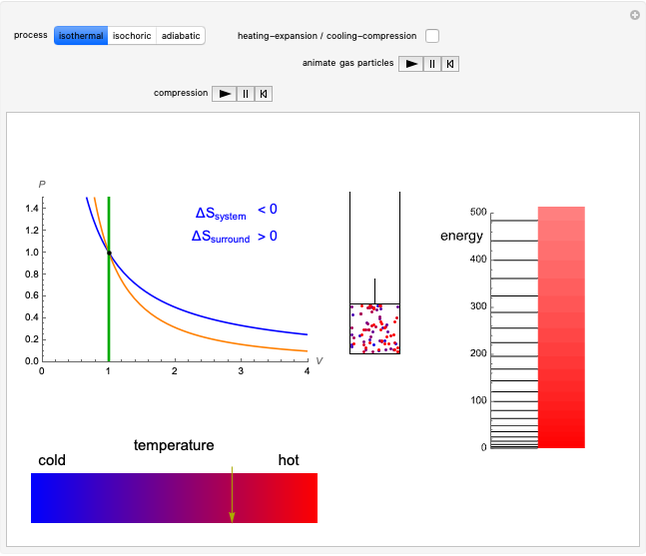
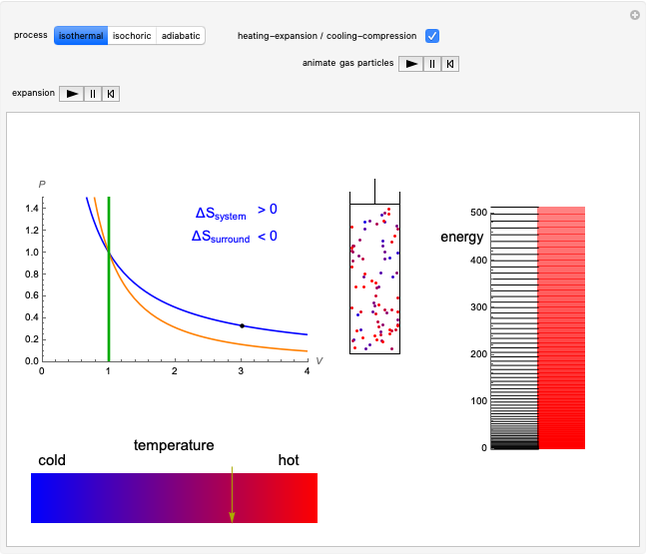
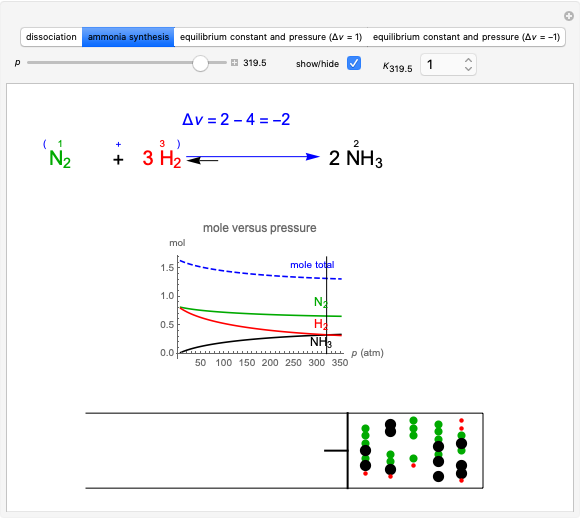
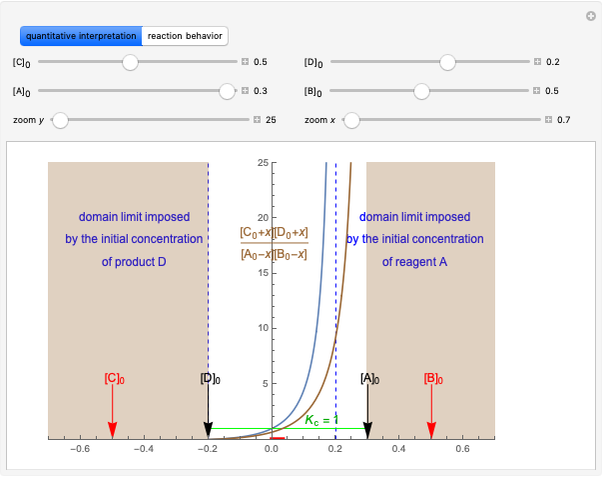
This Demonstration considers three different reversible processes from both a macroscopic and a microscopic point of view: isothermal expansion and compression, isochoric heating and cooling, and adiabatic expansion and compression [1]. Select the process, then use the checkbox to choose between heating–expansion or cooling–compression.

[more]

Use the "animate gas particle" button to start the animation. The temperature is indicated schematically on the color bar at the bottom.

At the top left is a pressure-volume plot for each process (isothermal in blue, isochoric in green and adiabatic in orange). Also shown are a piston and cylinder representing these processes. At the right is a schematic representation of the energy level distribution.

Global entropy is defined as the sum of the system entropy variation of the piston and the surrounding entropy variation . In a reversible processes .

When the system entropy change is positive, the entropy change of the surroundings must be negative, and vice versa. Both entropy changes are equal to 0 only in an adiabatic process.

[less]

Contributed by: D. Meliga, A. Ratti, L. Lavagnino and S. Z. Lavagnino (August 2022)
Open content licensed under CC BY-NC-SA

Snapshots

Details

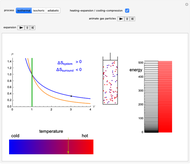
Snapshot 1: Isothermal expansion. At constant temperature, expanding the volume causes a compression in the energy-level spacing. As a consequence, more levels are occupied and the system entropy increases ).

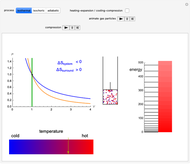
Snapshot 2: Isochoric heating. As the energy levels remain unchanged, rising temperature causes increased occupation of higher energy levels. The system entropy thus increases ).

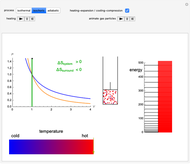
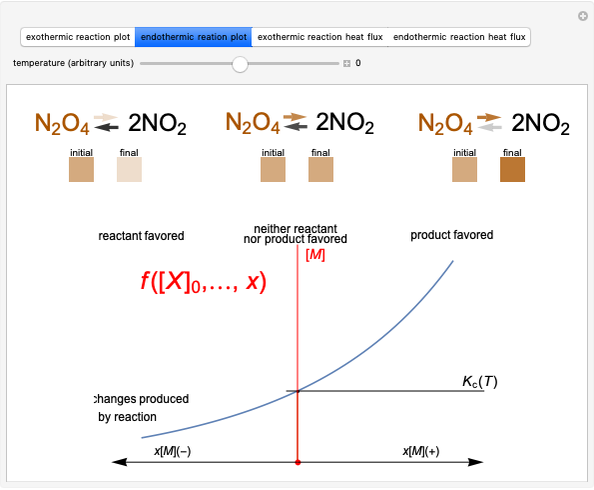
Snapshot 3: Adiabatic expansion. Expansion in volume causes a decreased spacing of the levels. A decrease in temperature leads to decreased occupancy of higher levels. The two effects compensate and the entropy remains constant , ).

Reference

[1] P. Atkins and L. Jones, Chemical Principles: The Quest for Insight, New York: W. H. Freeman, 1999.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send